树是一种典型的数据结构(逻辑结构),可以用来描述分支结构,属于一种分层、非线性结构。树的定义是递归的,因此树是一种递归的数据结构。每个结点有唯一的前驱结点,有一个或多个后继结点。($n$个节点有$n-1$条边)
基本术语:
- 度:结点的子结点的个数;
- 树的度:树种最大的度数;
- 分支结点:度大于$0$的结点;
- 叶子结点:度为$0$的结点;
- 结点层次:根结点为第一层,往下递增;
- 结点高度:从叶结点开始自底向上逐层累加;
- 结点深度:从根结点自顶向下逐层累加;
- 树的高度(深度):树中结点的最大层数;
- 有序树:从左到右,子树有序;交换子结点位置树不同;
- 无序树:交换子结点后树是相同的;
- 路径:两个结点之间所经过的节点序列,不包含边;路径是自上而下的(树的分支是有向的:从双亲指向孩子);
- 路径长度:路径上经历的边的数量;
- 森林:m棵互不相交的树的集合;
性质:
树中的结点数=所有结点度数(等价于所有的非根结点数)$+1$
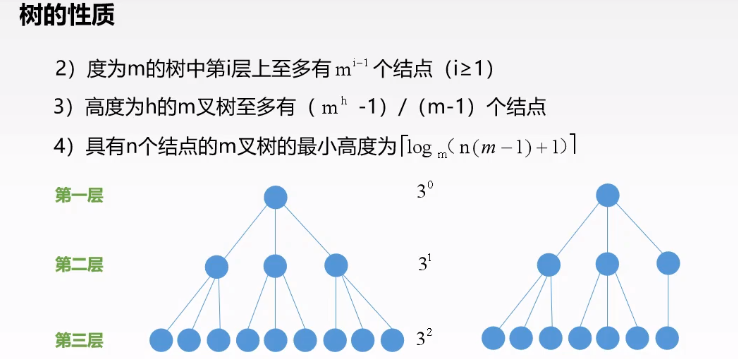
度为$m$的树中第$i$层至多有:$m^{i-1}$个结点
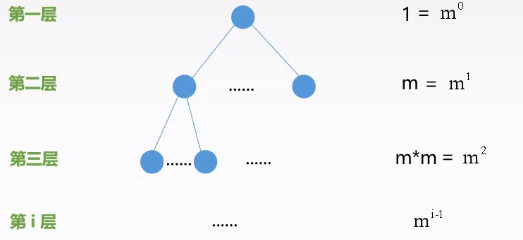
高度为$h$的$m$叉树至多有$(m^h-1)/(m-1)$个结点
具有$n$个结点的$m$叉树的最小高度为$log_m(n(m-1)+1)$(向上取整)
二叉树:
五种基本形态:空树、根节点、根节点-左子树、根节点-右子树、根节点-左子树-右子树
二叉树 vs 度为2的有序树:
- 二叉树可以为空,度为2的有序树至少有3个结点
- 二叉树孩子结点有左右之分,度为2的有序树的孩子结点次序是相对的(一个结点的时候,不区分左右)
特殊二叉树:
满二叉树:高度为$h$,含有$2^h-1$个结点(公式$(m^h-1)/(m-1)$ ,$m=2$),每一层都有最多结点,最后一层全是叶子结点。结点$i$:左孩子$2i$,右孩子$2i+1$;孩子结点$i$存在,双亲编号为$i/2$ 取整数
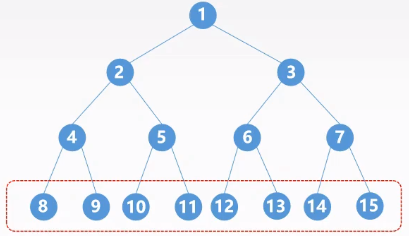
完全二叉树:高度为$h$,有$n$个结点的二叉树,当且仅当每个结点高度为$h$的满二叉树中编号$1-n$的结点一一对应(不能产生错位,即满二叉树的子集)。
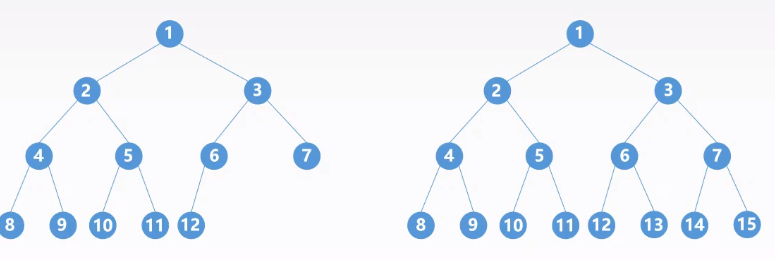
- 若$i\le n/2$,则结点$i$为分支结点,否则为叶子结点;($i=n/2$为最后一个结点的双亲结点,比该结点的双亲结点小,则为分支结点(1、2、3、4、5),大则为叶子结点(7、8、9、10、11、12))
- 叶子结点只可能在层次最大的两层上出现。对于最大层次的叶子结点(8、9、10、11、12),都一此排在左边位置上。
- 度为$1$的结点若存在,则可能有一个,且是编号最大的分支结点(6),并且孩子结点一定是左结点。
二叉排序树:一棵二叉树,若树非空则具有性质——对任意结点存在左子树或又子树,则其左子树上左右关键字均小于该结点,右子树上所有结点的关键字均大于该结点。
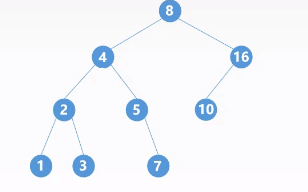
平衡二叉树:树上任意结点(非根节点)的左子树和右子树的深度之差不超过$1$(蓝色)。
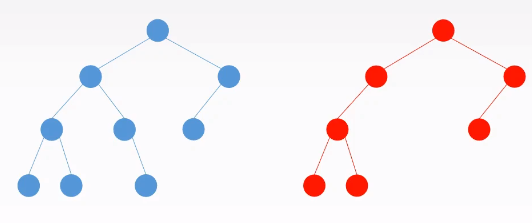
二叉树性质:
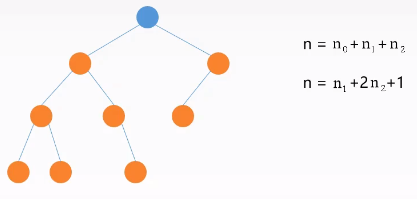
- 非空二叉树的叶子结点数等于度为$2$的结点数$+1$,即$n_0=n_2+1$。($n=n_0+n_1+n_2$)
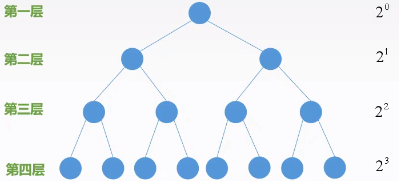
- 非空二叉树上第$k$层上至多有$2^(k-1)$个结点($k\geq0$)
- 高度为$h$的二叉树至多有$2^h-1$个结点($h\geq0$)