数据结构——二叉树的遍历

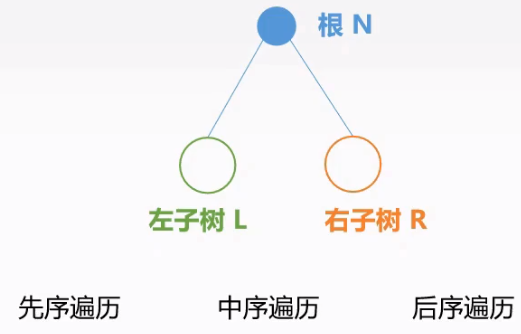
深度优先搜索

按某条路径访问树中每个结点，树的每个结点均被访问一次，而且之访问一次，包括先序遍历、中序遍历和后序遍历，这三种遍历都是深度优先遍历（DFS）。

递归算法非常简洁——推荐使用

当前编译系统优化效率很不错

特殊情况下使用栈模拟递归

理解编译栈的工作原理

理解深度优先遍历的回溯特点

有些应用环境资源限制不适合递归

先序遍历（PreOrder）

“中左右”的递归顺序：

访问根节点；
先序遍历左子树；
先序遍历右子树。

vector<int> preorderTraversal(TreeNode* root) {
        vector<int> res;
        vector<int> temp;
        
        if(!root) return {};
    
        res.push_back(root->val);
    
        temp=preorderTraversal(root->left);
        res.insert(res.end(),temp.begin(),temp.end());
    
        temp=preorderTraversal(root->right);
        res.insert(res.end(),temp.begin(),temp.end());  
        
        return res;
    }

时间复杂度：O(n)

中序遍历（InOrder）

“左中右”的递归顺序：

中序遍历左子树；
访问根节点；
中序遍历右子树。

vector<int> inorderTraversal(TreeNode* root) {
    vector<int> res;
    vector<int> temp;
    
    if(!root) return {};
    
    temp=inorderTraversal(root->left);
    res.insert(res.end(),temp.begin(),temp.end());
    
    res.push_back(root->val);
    
    temp=inorderTraversal(root->right);
    res.insert(res.end(),temp.begin(),temp.end());  
    
    return res;
}

时间复杂度：O(n)

后序遍历（PostOrder）

“左右中”的递归顺序：

后序遍历左子树；
后序遍历右子树；
访问根节点。

vector<int> postorderTraversal(TreeNode* root) {
        vector<int> res;
        vector<int> temp;
        
        if(!root) return {};
        
        temp=postorderTraversal(root->left);
        res.insert(res.end(),temp.begin(),temp.end());

        temp=postorderTraversal(root->right);
        res.insert(res.end(),temp.begin(),temp.end());  
        
        res.push_back(root->val);
        
        return res;
    }

时间复杂度：O(n)

递归算法转非递归算法——栈（前序遍历为例）

算法思想：

遇到一个结点，就访问该结点，并把此节点的非空右结点推入栈，然后下降取遍历它的左子树；
遍历完左子树后，从栈顶托出一个结点，并按照它的右链接指示的地址再去遍历该结点的右子树结构。

void PreOrder(BiTree T){
    InitStack(S);
    BiTree p = T;
    while(p||!isEmpty(S)){
        visit(p);
        if(p->rchild!=NULL)
            Push(S,p->rchild);
        if(p->lchild!-NULL)
            p=p->lchild;
        else{
            Pop(S,p);
        }
    }
}

递归算法转非递归算法——栈（中序遍历为例）

算法思想：

初始时依次扫描根结点的所有左侧结点并将它们——进栈；
出栈一个结点——访问它；
扫描该结点的右孩子结点并将其进栈；
依次扫描右孩子结点的所有左侧结点——进栈；
反复该过程直到栈为空。

void InOrder2(BiTree T){
    InitStack(S);
    BiTree p = T;
    while(p||!IsEmpty(S)){
        if(p){
            Push(S,p);	// 压栈
            p=p->lchild;	// 扫描左孩子
        }
        else{
            Pop(S,p);	// 弹出
            visit(p);	// 访问
            p=p->rchild;	// 扫描右孩子
        }
    }
}

递归算法转非递归算法——栈（后序遍历为例）

算法思想：

左子树返回 VS 右子树返回？
给栈中元素加上一个特征位
- $Left$ 表示已进入该结点的左子树，将从左边回来
- $Right$ 表示已进入该结点的右子树，将从右边回来

void PostOrder(BiTree T){
    PostStack(S);
    BiTree p = T;
    while(p||!IsEmpty(S)){
        while(p){
            
        }
    }
}

广度优先搜索

层次遍历——队列（先序遍历为例）

算法思想：

初始将根节点入队列并访问根结点；
若有左子树，则将左子树的根入队列；
若有右子树，则将右子树的根入队列；
然后出队列，访问该结点；
反复该过程直到队列为空为止。

vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int> > res;
        if(!root) return {};
        
        queue<TreeNode*> q;     // 初始化队列
        q.push(root);           // 根结点入队列 第一步
        
        while (!q.empty()) {
            int currentLevelSize = q.size();
            res.push_back(vector <int> ());
            
            for(int i=0;i<currentLevelSize;++i){        // 遍历
                auto node = q.front();
                q.pop();
                res.back().push_back(node->val);
                if (node->left)                         // 第二步
                    q.push(node->left);
                if (node->right)
                    q.push(node->right);                // 第三步
            }
        }
        return res;
    }

遍历序列构造二叉树

（后）先序遍历序列+中序遍历序列可以确定一棵二叉树，而后序遍历和先序遍历序列不可以确定一棵二叉树。

中序遍历和先序遍历序列：

先序遍历序列中，第一个结点时根结点；
根节点将中序遍历序列划分成为两部分；
再先序遍历中确定两部分的结点，两部分的第一个结点分别为左子树、右子树的根；
再子树递归重复过程中，便可以唯一确定一棵二叉树。

过程：

先序遍历序列中的第一个结点为二叉树根结点；在中序遍历序列中找出根结点——将中序遍历序列划分成：左子树中序遍历+右子树中序遍历；
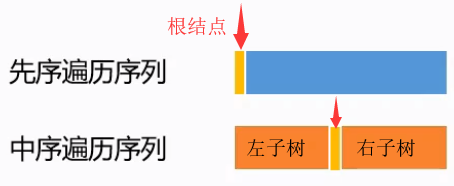
由左子树的遍历序列和右子树的遍历序列找出所有左子树结点和右子树结点，并在先序遍历中确立它们的位置；
继续执行该过程，找出左子树和右子树先序遍历的第一个结点：分别为左子树根结点和右子树根结点；
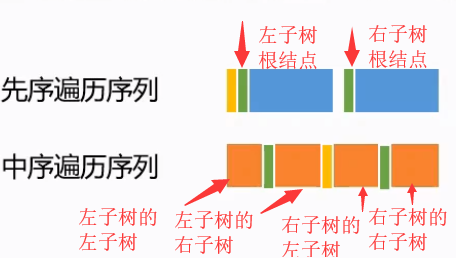
重复执行该过程，就可以确定一棵二叉树。

例子：

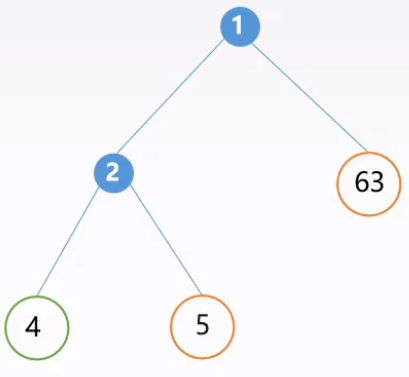
先序遍历：1，2，4，5，3，6；中序遍历：4，2，5，1，6，3。

找出先序遍历的第一个结点，为二叉树的根结点（1）；
在中序遍历中找到该结点，将其划分为左子树（4，2，5）和右子树（6，3）；
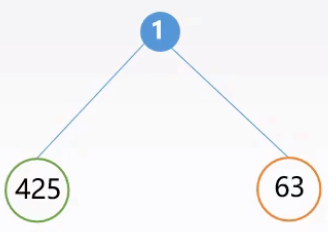
依次找出左子树的根结点（2），并在中序遍历序列中找到该结点的左子树（4）和右子树（5）；
按照同样的方法操作右子树，右子树根结点为 3，在中序遍历序列中找到该结点的左子树（6）和右子树（空）。

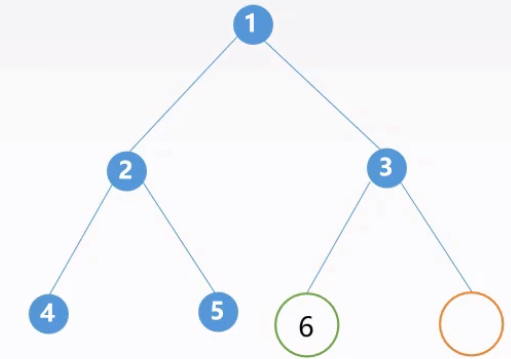
层次遍历序列和中序遍历序列也可以构造出二叉树。

leetcode重建二叉树

输入某二叉树的前序遍历和中序遍历的结果，请重建该二叉树。
假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

例如，给出
	前序遍历 preorder = [3,9,20,15,7]
	中序遍历 inorder = [9,3,15,20,7]
	
返回如下的二叉树：

    3
   / \
  9  20
    /  \
   15   7

限制：0 <= 节点个数 <= 5000

思路：

需要找中序遍历中元素的Index，可以建立值与Index的映射（哈希表）：Key=前序遍历的val；Value=中序遍历的Index，并对这个哈希表进行维护；
6个参数：前序——左、右子树的起始位置（preLeft，preRight）；中序——左、右子树对应的下标范围（preorder[]、inorder[]、inLeft、inRight）；