数据结构——树的存储结构

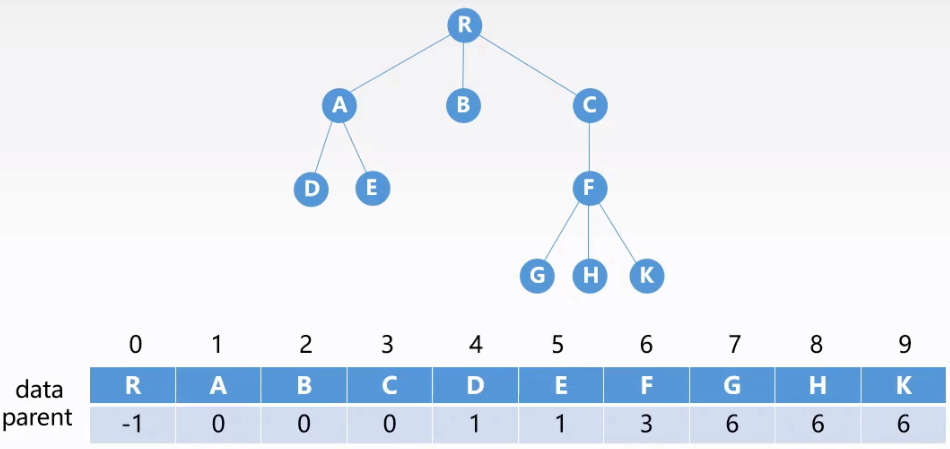
双亲表示法

采用一组连续的存储空间来存储每个结点，同时在每个结点中增设一个伪指针，指示双亲结点在数组中的位置，根结点的下表为$0$，其伪指针域为$-1$。

​

#define MAX_TREE_SIZE 100						
typedef struct{				// 每个结点					
    ElemType data;			// 结点数据					
    int parent;				// 结点双亲
}PTNode;
				
typedef struct{				// 树				
    PNOde nodes[MAX_TREE_SIZE];		// 结点结构体数组			
    int n;					// 结点数量
}PTree;

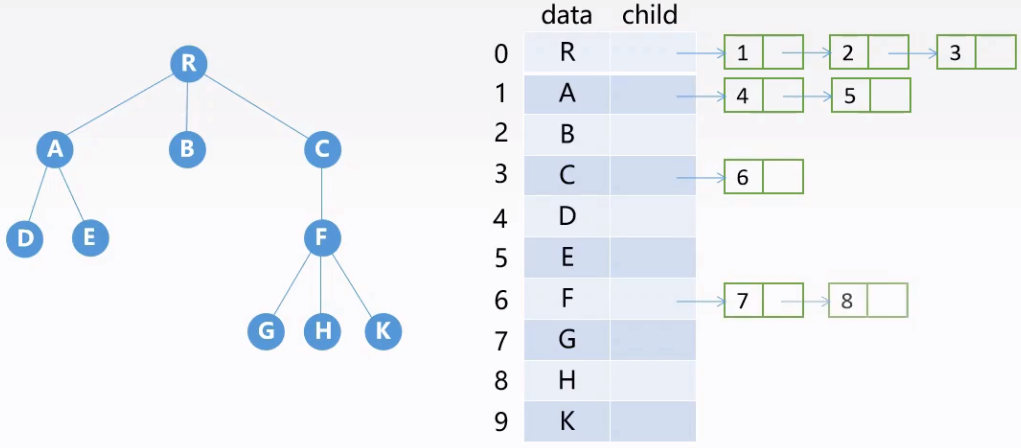
孩子表示法

将每个结点的孩子结点都用单链表连接起来形成一个线性结构，$n$个结点具有$n$个孩子链表。

#define MAX_TREE_SIZE 100				
typedef struct{			// 孩子结点结构体			
    int child;			// 孩子结点下标					
    struct CNode *next;	// 下一个孩子结点的指针
}CNode;
							
typedef struct{			// 每一个结点存放的数据元素			
    ElemType data;		// 结点数据
    struct CNode *child;// 对应的第一个孩子结点的指针——单链表头指针
}PNode;
							
typedef struct{			// 树结构			
    PNode nodes[MAX_TREE_SIZE];	// 结点数量
    int n;				// 结点数组
}CTree;

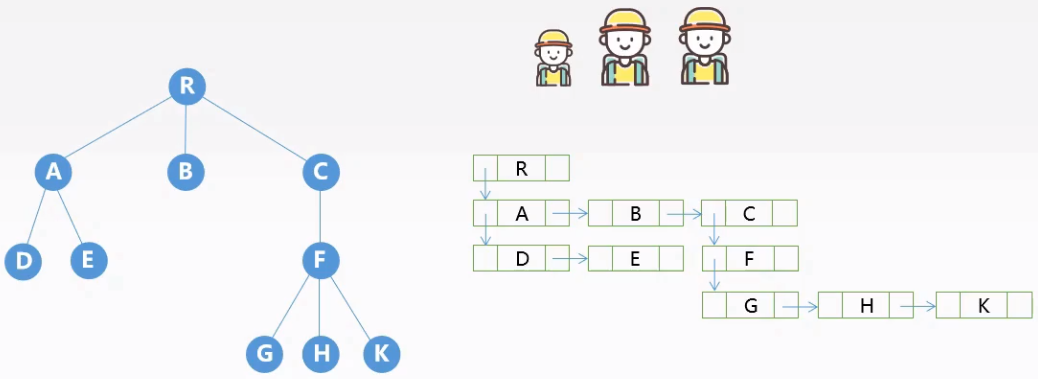
孩子兄弟表示法

以二叉链表作为树的存储结构，又称二叉树表示法（左孩子右兄弟）。

typedef struct CsNode{
    ElemType data;
    struct CSNode *friendchild, *nextsibling;
}CSNode,CSTree;

根结点右指针为空——没有兄弟结点

区别与联系

方法	优点	缺点
双亲表示法	寻找结点双亲结点效率高	寻找结点的孩子结点效率低
孩子表示法	寻找结点的孩子结点效率高	寻找结点的双亲结点效率低
孩子兄弟表示法	寻找结点的孩子结点效率高 方便实现树转换为二叉树	寻找结点的双亲结点效率低