数据结构——树的应用并查集

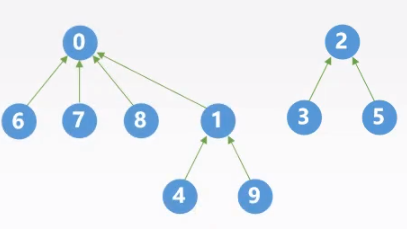
定义

一种简单的几何表示：一个集合有若干个元素，该集合也被划分成若干个子集。通常用树的双亲表示法（用数组存放每个结点的元素，用伪指针存储该结点双亲结点的索引）作为并查集的存储结构。

通常用数组元素的下标表示元素名，用根结点的下标代表子集合名，根结点的双亲结点表示负数。

应用

初始化——Initial(s)

功能：将集合$S$的每个元素都初始化为只有一个单元素的子集合。

并——Union(S, Root1, Root2)

功能：把集合$S$中的子集合（互不相交）$Root2$并入子集合$Root1$。

查——Find(S,x)

查找集合$S$中单元素$x$所在子集合，并返回该子集合的名字。

例子

$$S={0,1,2,3,4,5,6,7,8,9}$$

$S_0={0}，S_1={1}，S_2={2}，S_3={3}，S_4={04}，$

$S_5={5}，S_6={6}，S_7={7}，S_8={8}，S_9={9}。$

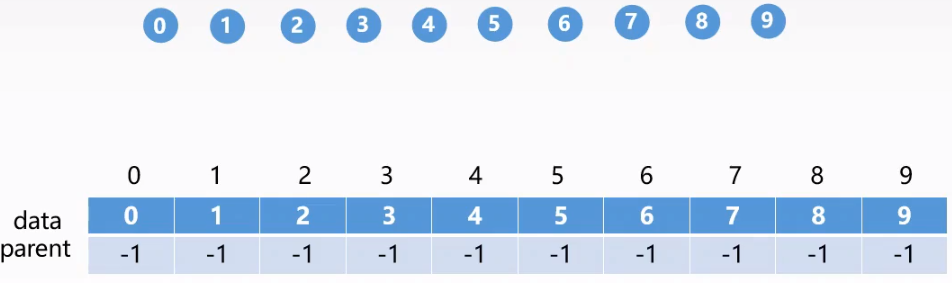
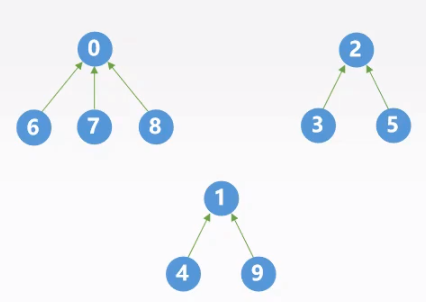
$S_0={0，6，7，8}，S_1={1，4，9}，S_2={2，3，5}$

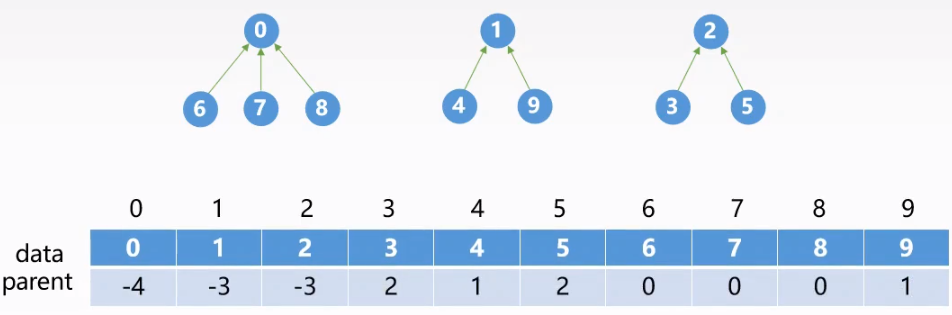
语言实现

Initial()

#define SIZE 100
int UFSet[SIZE];

void Initial(int S[]){		// 初始化每个元素为子集合
    for(int i=0;i<size;++i){
        S[i]=-1;			// 将双亲结点的下标修改为-1
    }
}

Find()

int Find(int S[], int x){
    while(S[x]>=0)		// 双亲指针不断向上查找
        x=S[x];
    return x;			// 返回该元素所在的根结点的数组下标
}

Union()

void Union(int S[], int Root1, int Root2){
    S[Root2]=Root1;
}