树、森林与二叉树的转换
树转换二叉树
规则:左孩子右兄弟,每个结点左指针指向它的第一个孩子结点,右指针指向它在树中相邻兄弟结点。
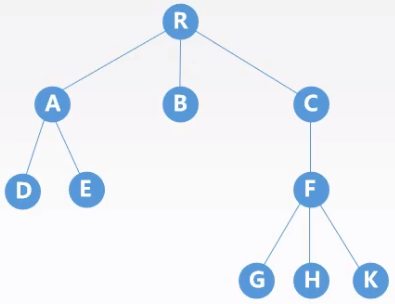
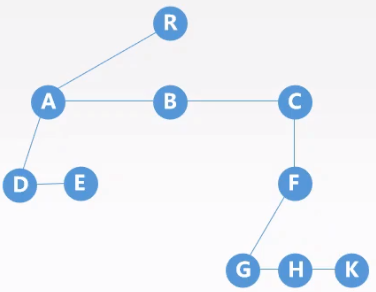
二叉树转换为树
规则: 逆过程,将指针修改回来,指向其双亲结点。
森林转换二叉树
二叉树转换森林是唯一的
规则:将每一棵树转换为二叉树,将每棵二叉树的根依次作为上一棵二叉树的右子树。
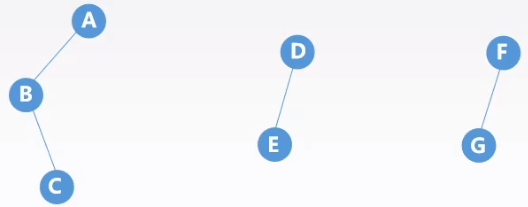
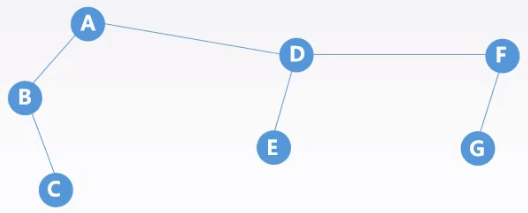
二叉树转换森林
规则:逆过程,先找到每一棵树,拆解。
树、森林的遍历
树的遍历
规则:按照某种方式访问树中的每个结点,且仅访问依次。
先根遍历:若树非空,则先访问根结点,再按从左往右的顺序遍历根结点的每个子树,即:R、A、D、E、B、C、F、G、H、K——与二叉树先序遍历序列相同。
树的先根遍历序列与这棵树对应的二叉树先序遍历序列相同
后根遍历:若树非空,则先按从左往右的顺序遍历根结点的每棵子树,再访问根结点,即:D、E、A、B、G、H、K、F、C、R——与二叉树中序遍历序列相同。
树的后根遍历序列与这棵树对应的二叉树中序遍历序列相同
层次遍历:
森林的遍历
先序遍历
若森林非空,则
- 访问森林中第一棵树的根结点
- 先序遍历第一棵树的子树森林
- 先序遍历除去第一棵树之后剩余的树构成的子树森林
中序遍历
若森林非空,则
- 中序遍历第一棵树的根结点的子树森林
- 访问森林中第一棵树的根结点
- 中序遍历除去第一棵树之后剩余的树构成的子树森林
例子
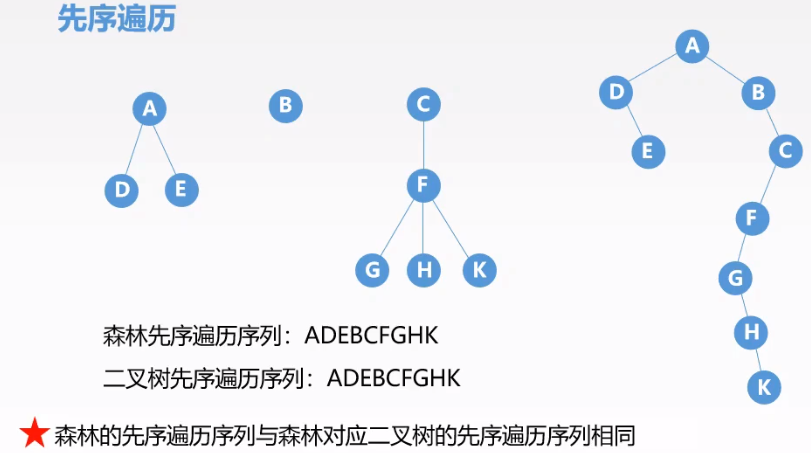
先序遍历:A、D、E、B、C、F、G、H、K
森林的先序遍历序列与森林对应的二叉树先序遍历序列相同
中序遍历:D、E、A、B、G、H、K、F、C
森林的中序遍历序列与森林对应的二叉树先中序历序列相同
对应关系
| 树 | 森林 | 二叉树 |
|---|---|---|
| 先根遍历 | 先序遍历 | 先序遍历 |
| 后根遍历 | 中序遍历 | 中序遍历 |

