数据结构——哈夫曼树

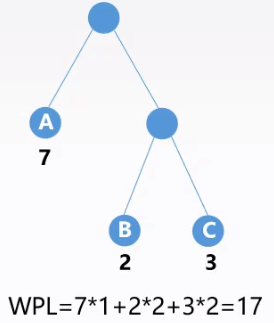
相关定义

1. 路径长度：路径上所经历边的个数
2. 结点的权：结点被赋予的数值
3. 树的带权路径长度：WPL，书中所有叶结点的带权路径长度之和，记为：

$$WPL=\sum_{i=0}^{n} w_i l_i$$

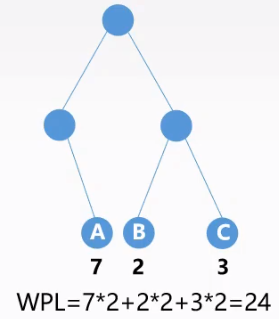
叶节点个数相同，但是树的带权路径长度不一定相同！

哈夫曼树

定义：最优二叉树，含有$n$个带权叶子结点带权路径长度最小的二叉树

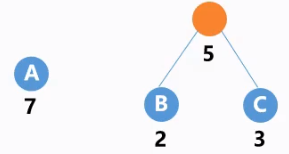
构造

1. 将$n$个结点作为$n$棵仅含有一个根结点的二叉树，构成森林$F$;
2. 生成一个新的结点，并从$F$中找出权值最小的两颗树作为它们的左子树和右子树，且新结点的权值为两棵子树根结点的权值之和；
3. 从$F$中删除这两个数，并将新生成的数假如到$F$中；
4. 重复步骤2、3，直到$F$中只有一棵树为止。

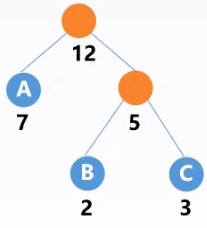
性质

1. 每个初始结点都会成为叶子结点，双支结点都为新生成的结点
2. 权值越大离根结点越近，反之离根结点越远
3. 哈夫曼树中没有结点的度为$1$（叶子节点：$0$，分支结点：$2$）
4. $n$个叶子结点的哈夫曼树的结点总数为$2n-1$,其中度为$2$的结点数位$n-1$

应用

编码问题

对于一个字符串序列，用二进制来表示字符。

固定长度编码：每一个字符对应的二进制长度相同

HelloWorld

000001010010011100011101010110

000——H；001——e；010——l ；011——o

100——W；101——r；110——d

可变长度编码：每一个字符对应二进制长度可变

HelloWorld

0001001101110000

ll/H

00——H；01——e；0——l；1——o；

10——W；11——r；000——d；

前缀编码：没有一个编码是另一个编码的前缀

HelloWorld

000001111101110001110111010

000——H；001——e；11——l；011——o；

100——W；101——r；010——d；

哈夫曼树——编码

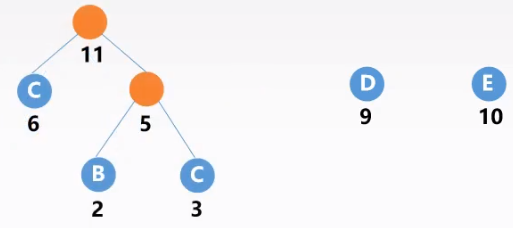
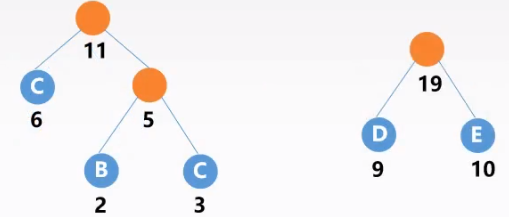
出现次数：

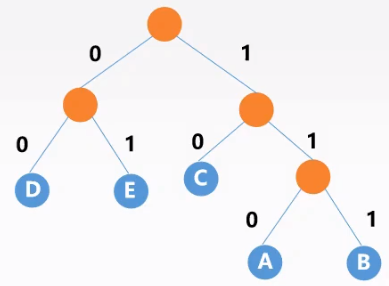
A：2；B：3；C：6；D：9；E：10

利用哈夫曼树的构造过程，将所有的边赋予左边的边$0$、右边的边$1$：A——110；B——111；C——10；D——00；E——01

出现次数越多的结点越靠近根结点，因此编码更短；反之越远离根结点，编码长度越长。

哈夫曼树并不唯一，所以每个字符对应的哈夫曼编码也不唯一（左右子树可以交换），但带权路径长度相同且最优