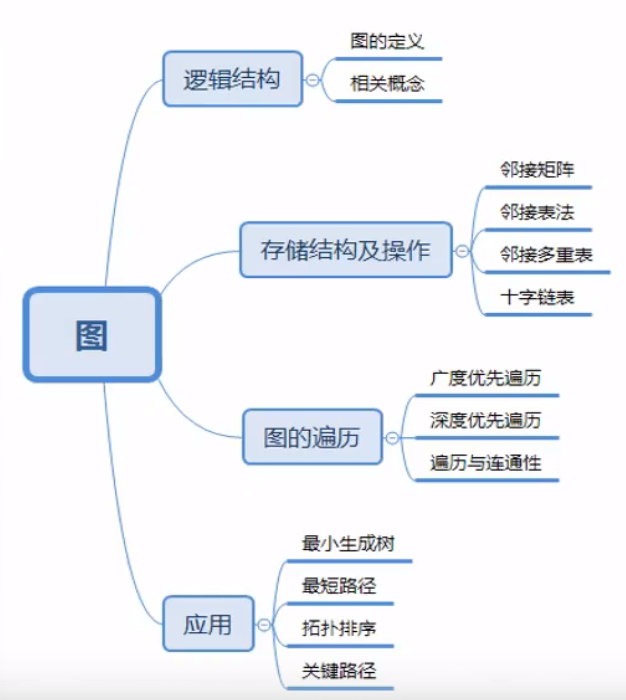
基本概念
- 定义:图$G$有顶点集$V$和边集$E$组成,记为$G=(V,E)$,其中$V(G)$表示图$G$中顶点的有限非空集;$E(G)$表示图$G$中顶点之间的关系(边)集合。
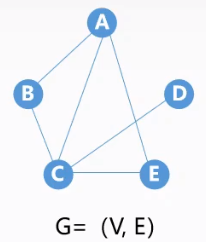
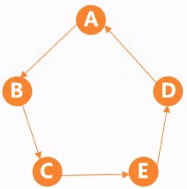
- 顶点集:$V={A,B,C,D,E}$,$|V|=5$
- 边集:$E={(A,B),(A,C),(A,E),(B,C),(C,D),(C,E)}$,$|E|=6$
线性表、树可以为空,但是图不能为空! - 术语:$|V|$表示图$G$中顶点的个数,也称图$G$的阶;$|E|$表示图$G$中边的条数
- 顶点的度:以该顶点为端点的边的数目
无向图&有向图
| 无向图 | 有向图 |
|---|---|
 |
 |
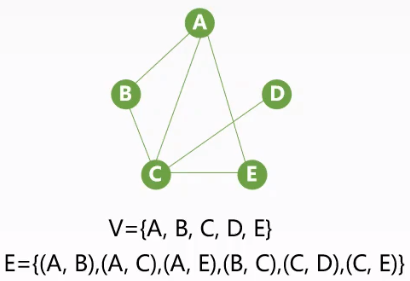
| 无向边:$v$——$w$ 无序对:$(v, w)=(w, v)$,$v,w$互为邻接点。 |
有向边:$v$——>$w$ 有序对:<$v,w$>$\neq$ <$w,v$>,$v$邻接到$w$,$w$邻接自$v$。 |
| 顶点的度 | |
| 以$v$为端点的边的个数——$TD(v)$ $n$顶点,$e$条边无向图度的总数:$\sum_{i=1}^nTD(v_i)=2e$ |
出度:以$v$为起点的有向边的条数——$OD(v)$ 入度:以$v$为终点的有向边的条数——$ID(v)$ 顶点$v$的度:$TD(v)=ID(v)+OD(v)$ $n$顶点,$e$条边有向图出度、入度满足:$\sum_{i=1}^nID(v_i)=\sum_{i=1}^nOD(v_i)=e$ |
| 连通 | 强连通 |
 |
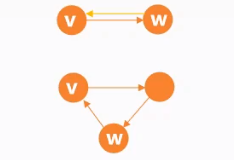 |
| 若从顶点$v$到顶点$w$有路径(不一定是边)存在,则称$v$和$w$是连通 | 若从顶点$v$到顶点$w$和顶点$w$到顶点$v$都有路径(不一定是边)存在,则称$v$和$w$是强连通 |
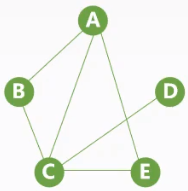
| 连通图 | 强连通图 |
 |
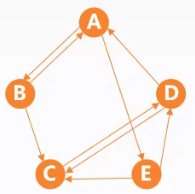 |
| 任意两个结点之间都是连通的 | 任意两个结点之间都是强连通的 |
| $n$个顶点最少有$(n-1)$条边 | $n$个顶点最少有$n$条边 |
 |
 |
简单图&多重图
| 简单图 | 多重图 |
|---|---|
 |
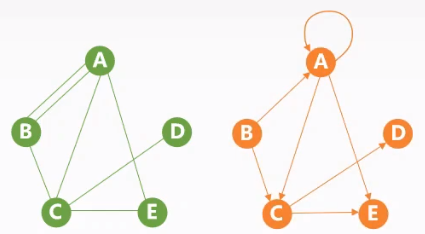 |
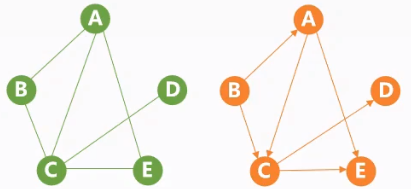
| 无重复边,不存在结点到自身 | 存在重复边,或存在结点到自身的边 |
完全图
| 无向完全图 | 有向完全图 |
|---|---|
 |
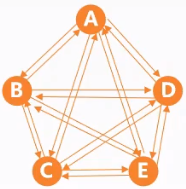 |
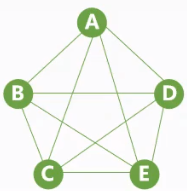
| 任意两个顶点之间都存在边 | 任意两个顶点之间都存在方向相反的弧 |
| $n$个顶点有$n(n-1)/2$条边 | $n$个顶点有$n(n-1)$条边 |
子图
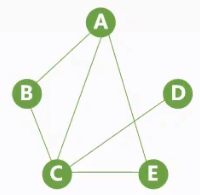
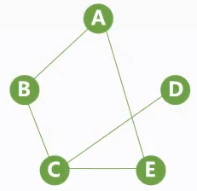
- 定义:设有两个图$G=(V,E)$和$G’=(V’,E’)$,若V’是V的子集,且$E’$是$E$的子集,则称$G’$是$G$的子图(原图也是其子图,只有顶点没有边也称为子图);且若$V(G)=V(G’)$则称$G’$为$G$的生成子图。
| 图 | 子图 | 生成子图 |
|---|---|---|
 |
 |
 |
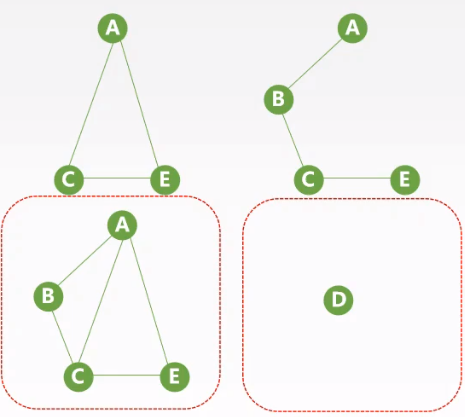
连通分量与&强连通分量:
连通分量——极大连通子图
强连通分量——极大强连通子图
定义:对于$G$的一个(强)连通子图$G’$,如果不存在$G$的另一个(强)连通子图$G’’$,使得$G’\subset G’’$,则称$G’$为$G$的(强)连通分量。
| 无向图 | 有向图 |
|---|---|
 |
 |
| 连通分量 | 强连通分量 |
 |
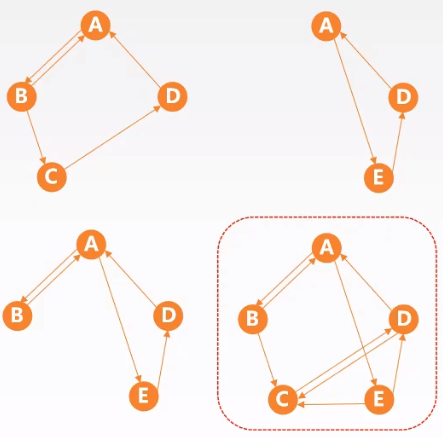 |
非连通图的连通分量有多个,连通图的连通分量就是自身。
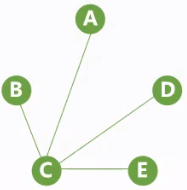
生成树、生成森林
连通图只能生成生成树,非连通图只能生成生成森林。
| 连通图 | 极小连通子图:连通子图且包含边最少 | 生成树:连通图包含全部顶点的一个极小连通子图 |
|---|---|---|
 |
 |
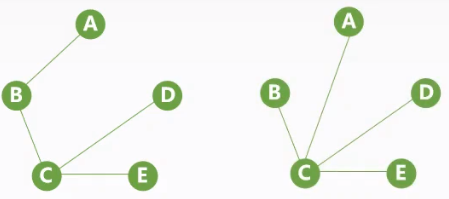 |
$n$个顶点图的生成树有$n-1$条边
| 非连通图 | 连通分量 | 生成森林:非连通图所有连通分量的生成树组成生成森林 |
|---|---|---|
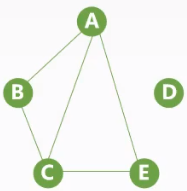 |
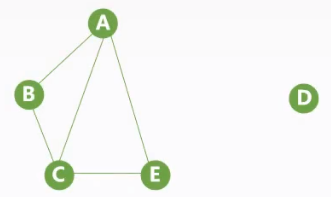 |
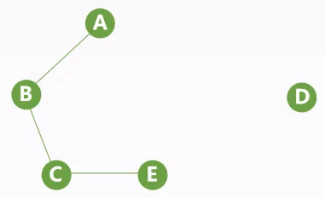 |
网
定义:为边增加权重(分析路径问题)

稠密图&稀疏图
稠密稀疏的界定:$|E|<|V|\cdot log(|V|)$
| 稠密图——边多 | 稀疏图——边少 |
|---|---|
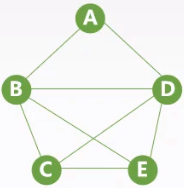 |
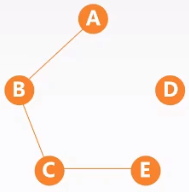 |
有向树
定义:一个顶点的入度为$0$,其余顶点的入度均为$1$的有向图
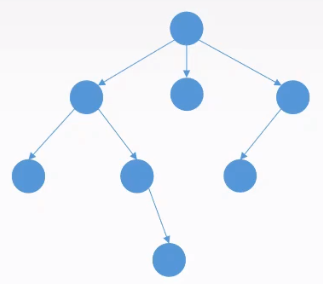
与树的区别:树的度为孩子结点的个数,有向树的度是出度+入度,有向树实则为图。
路径&路径长度&回路
路径定义:图中顶点$v$到顶点$w$的顶点序列,序列中顶点不重复的路径称为简单路径。
路径长度:路径上边的数目,若该路径最短则称其为距离。
回路:第一个顶点和最后一个顶点相同的路径。
| 无向图 | 有向图 |
|---|---|
 |
 |
| $A$——>$D$的一条路径:$A$——>$C$——>$D$ $D$——>$A$的一条路径:$D$——>$C$——>$A$ 路径长度:2 一条回路:$A$——>$C$——>$E$——>$A$ |
$A$——>$D$的一条路径:$A$——>$E$——>$D$ $D$——>$A$的一条路径:$NULL$ 路径长度:2 一条回路:$A$——>$B$——>$A$ |

