数据结构——图的存储与操作

图的存储结构

邻接矩阵法

1. 结点数为$n$的图$G=(V,E)$的邻接矩阵$A$是$n\times n$的。
2. 将$G$的顶点编号为$V_1$，$V_2$，$V_3$，…，$V_n$（数组下标）
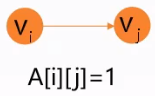
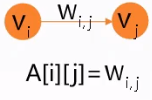
3. 若<$V_i,V_j$>$\in E$，则$A[i][j]=1$，否则$A[i][j]=0$。

$$A[i][j]=\begin{cases} 1 & 若(V_i,V_j)或<V_i,V_j>是E(G)中的边 \\ 0 & 若(V_i,V_j)或<V_i,V_j>不是E(G)中的边 \end{cases}$$

无向图&有向图

无向图	有向图
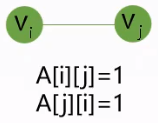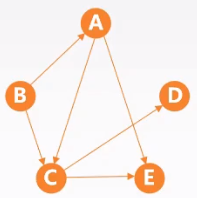
$V={A,B,C,D,E}$ $E={(A,B),(A,C),(A,E),(B,C),(C,D),(C,E)}$	$V={A,B,C,D,E}$ $E$={<$B$,$A$>,<$A$,$C$>,<$A$,$E$>,<$B$,$C$>,<$C$,$D$>,<$C$,$E$>}

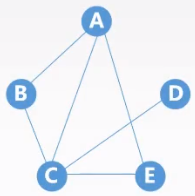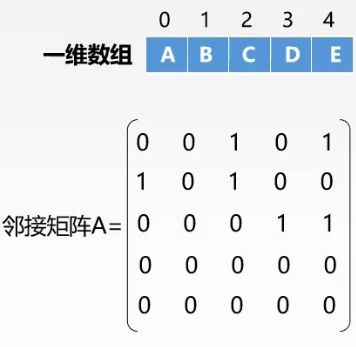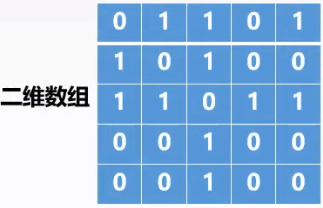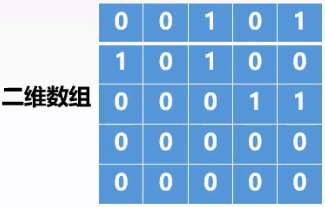网

1. 结点数为$n$的图$G=(V,E)$的邻接矩阵$A$是$n\times n$的。
2. 将$G$的顶点编号为$V_1$，$V_2$，$V_3$，…，$V_n$（数组下标）
3. 若<$V_i,V_j$>$\in E$，则$A[i][j]=w_{i,j}$，否则$A[i][j]=\infty$。

$$A[i][j]=\begin{cases} w_{i,j} & 若(V_i,V_j)或<V_i,V_j>是E(G)中的边 \\ A[i][j]=\infty & 若(V_i,V_j)或<V_i,V_j>不是E(G)中的边 \end{cases}$$

无向网
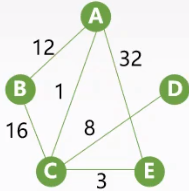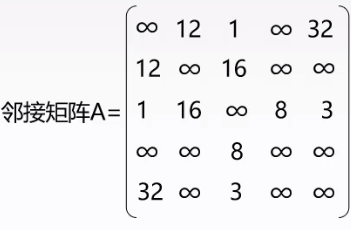1. 邻接矩阵法的空间复杂度为$O(n^2)$，适用于稠密图 2. 无向图的邻接矩阵为对称矩阵 3. 无向图中第$i$行（或第$j$列）非$0$元素（非正无穷）的个数为第$i$个顶点的度； 4. 有向图中第$i$行（第$j$列）非$0$元素（非正无穷）的个数为第$i$个顶点的出度（入度）

邻接矩阵运算

设图$G$的邻接矩阵为$A$，矩阵运算$A^n$的含义？

$A^2$的含义	$A^n$的含义

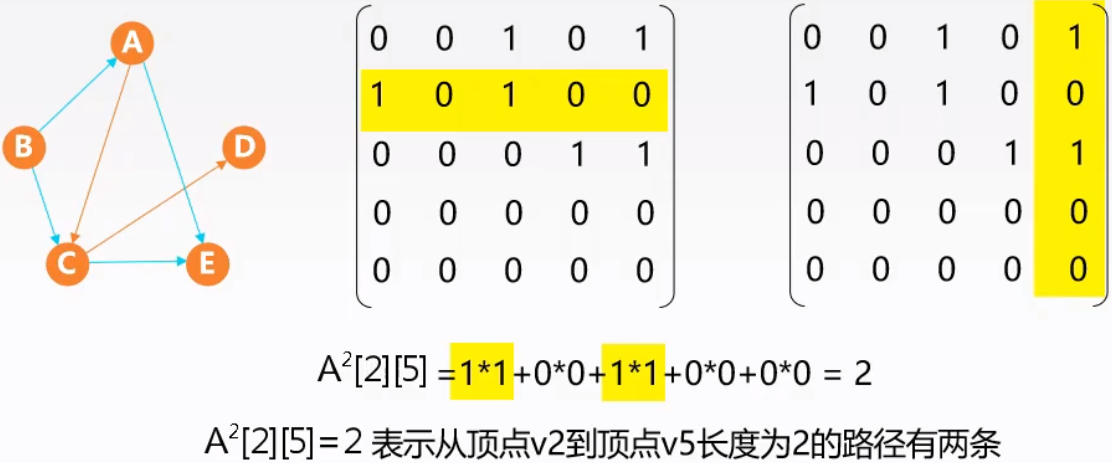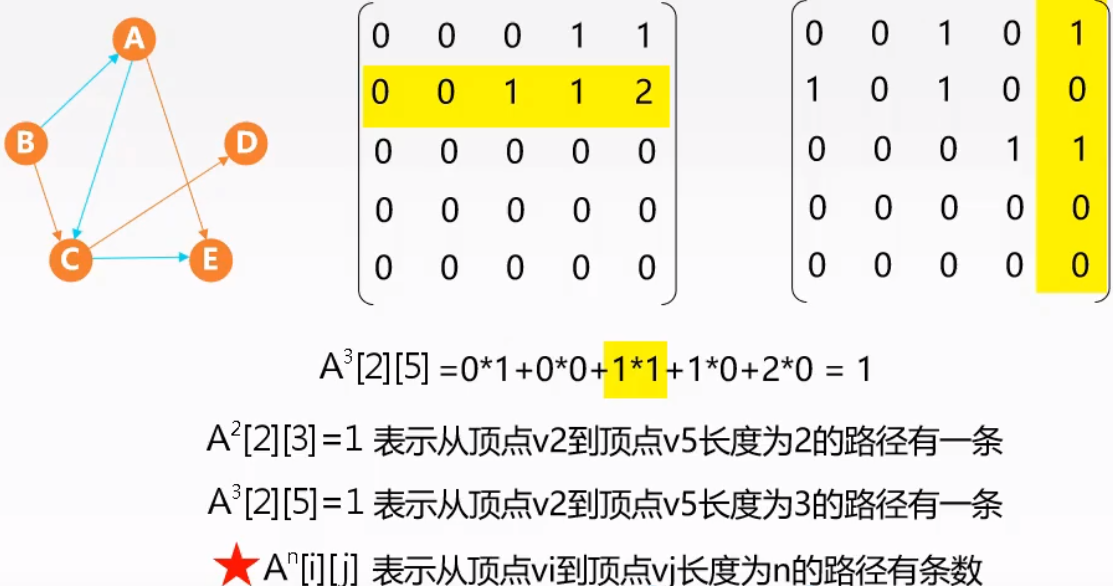邻接表法

1. 定义：为每个顶点建立一个单链表存放与它相邻的边
2. 顶点表：采用顺序存储，每个数组存放顶点的数据和边表的头指针
3. 边表（出边表）：采用链式存储，单链表中存放与一个顶点相邻的所有边，一个链表节点表示一条从该顶点到链表节点顶点的边（有向图有方向）

顶点表节点	边表节点

需要有边的存在则建立，可节省空间

有向图	无向图

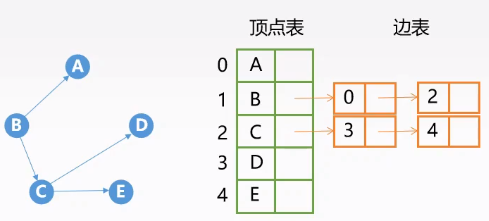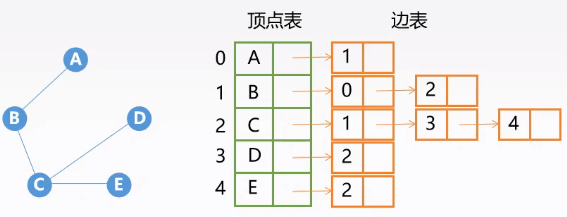1. 代码定义：

// 边表节点
typedef struct ArcNode{
    int adjvex;				// 边的节点
    struct ArcNode* next;	// 下一条边
    // InforType info;		// 边权值
}ArcNode;
// 顶点节点
typedef struct VNode{
    VertexType data;		// 顶点数据
    ArcNode* first;			// 边表头节点
}VNode,Adjust[MaxVertexNum];
// 邻接表
typedef struct{
    AdiList vetices;
    int vexnum,arcnum;
}ALGraph

1. 特点：无向图——存储空间$O(|V|+|2E|)$；有向图——存储空间$O(|V|+|E|)$；适用于稀疏图；邻接表不唯一

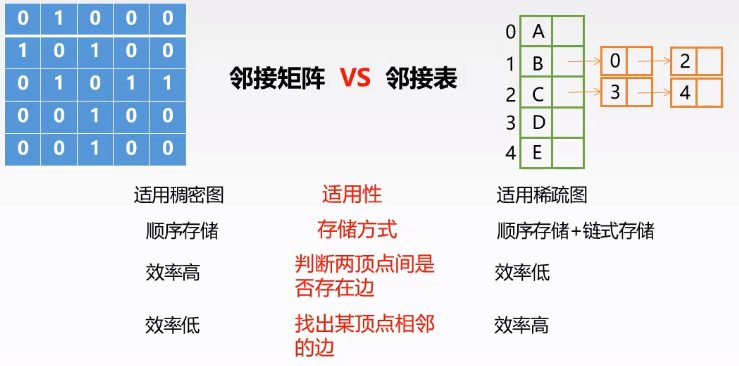
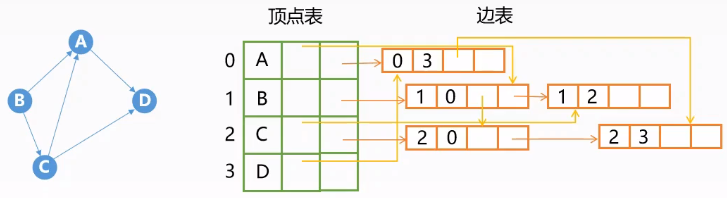
十字链表法

定义：有向图的一种链式存储结构，为了快速寻找出边和入边。即保存出边，又保存入边

顶点表节点	边表节点

typedef struct ArcNode{
    int tailvex,headvex;
    struct ArcNode* hlink,*tlink;
    // InforType info;
}
typedef struct VNode{
    VertexType data;
    ArcNode* firstin,*firstout;
}
typedef struct{
    VNode xlist[MaxVertexNum];
    int vexnum,arcnum;
}GLGraph;

邻接多重表法

图的基本操作

广度优先搜索

深度优先搜索