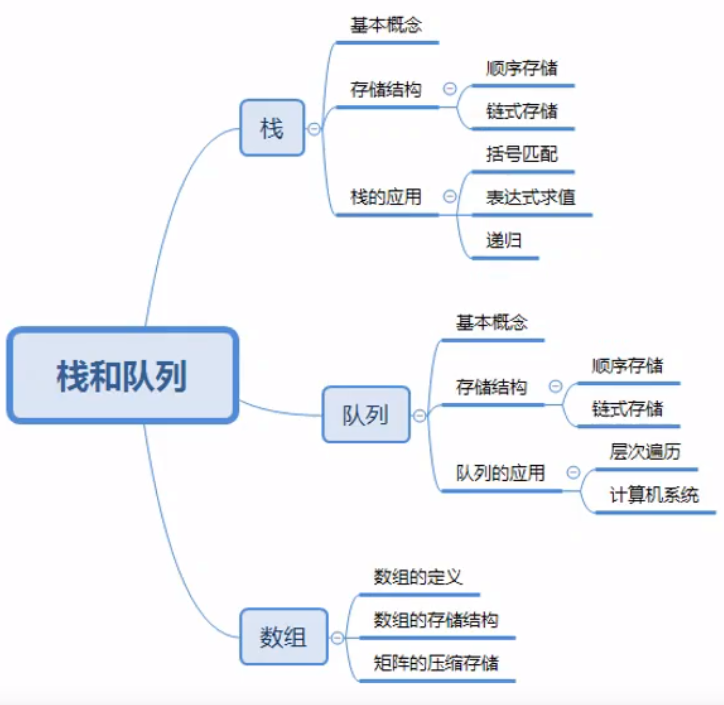
栈（stack）——后进先出（LIFO）

定义

只允许在一端进行插入或删除操作的受限线性表

栈顶（top）：可以出栈的一端

栈底（bottom）：无法出入栈的一端

入栈：$s=(a_1,a_2,a_3,a_4,a_5)$，出栈：$(a_5,a_4,a_3,a_2,a_1)$

基本操作

初始化（InitStack(&S)）——初始化一个空栈S

1
2
3

void InitStack(SqStack &S){
    S.top=-1;
}

判空（StackEmpty(S)）——判断一个栈是否为空，若栈为空则返回true，否则返回false

bool StackEmpty(SqStack S){
    if(S.top==-1)
        return true;
    else
        return false;
}

进栈（Push(&S,x)）——若栈S未满，则将x加入栈使之成为新的栈顶

bool Push(SqStack &S, ElemType x){
    if(S.top==MaxSize-1)
        return false;
    S.data[++S.top]=x;		// 先对top加1操作，再进行赋值
    return true;
}

出栈（Pop(&S,&x)）——会删除——若栈S非空，则弹出栈顶元素，并用x返回

bool Pop(SqStack &S, ElemType x){
    if(S.top==-1)
        return false;
    x=S.data[S.top--];		// 先给x赋值，再对top减1
    return true;
}

读取栈顶（GetTop(S,&x)）——不会删除——读取栈顶元素，若栈S非空则用x返回栈顶元素

bool GetTop(SqStack S, ElemType &x){
    if(S.top==-1)
        return false;
    x=S.data[S.top];
    return true;
}

存储结构

顺序存储结构

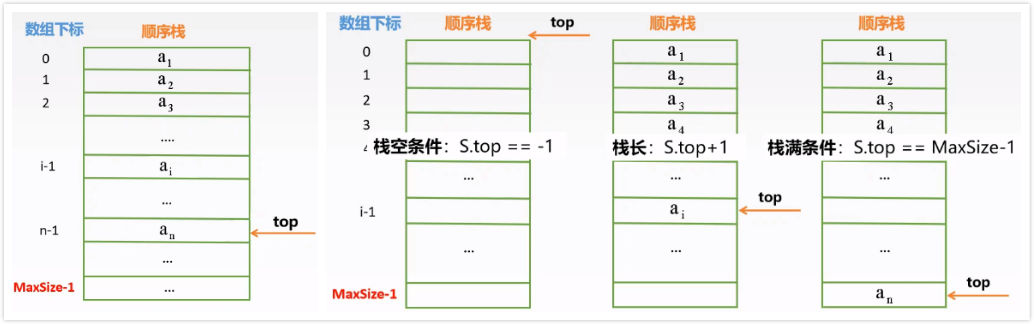
typedef struct{
    ElemType data[MaxSize];
    int top;
}SqStack'

共享栈——将两个栈底设置在共享空间的两端，栈顶向空间中间延伸

判空：0号栈top==-1，1号栈top==MaxSize

栈满：top1-top0==1

优点：存取复杂度$O(1)$，但空间利用更有效

链式存储结构

定义：采用链式存储的栈（类似单链表，表头节点为栈顶，所有操作在表头进行）

typedef struct LinkNode{
    ElemType data;
    struct LinkNode *next;
}*LiStack;

队列（Queue）——先进先出（FIFO）

定义

只能在表的一端进行插入，在另一端进行删除的线性表

队头操作：出队

队尾操作：入队

基本操作（循环队列）

初始化（InitQueue(&Q)）——初始化队列，构造一个空队列

1
2
3

void InitQueue(SqQueue &Q){
    Q.rear=Q.front=0;
}

判空（QueueEmpty(Q)）——判断队列是否为空，若为空返回true，否则返回false

bool isEmpty(SqQueue Q){
    if(Q.rear==Q.front)
        return true;
    else
        return false;
}

入队（EnQueue(&Q,x)）——若队列Q非空，则将x加入使之成为新的队尾

// 方法1
bool EnQueue(SqQueue &Q, ElemType x){
    if((Q.rear+1)%MaxSize==Q.front)
        return false;
    Q.data[Q.rear]=x;
    Q.rear=(Q.rear+1)%MaxSize;
    return true;
}

出队（DeQueue(&Q,&x)）——若队列Q非空，则删除对头元素，并用x返回

// 方法1
bool DeQueue(SqQueue &Q, ElemType &x){
    if(Q.rear==Q.front)
        return false;
    x=Q.data[Q.front];
    Q.front=(Q.front+1)%MaxSize;
    return true;
}

读取队头（GetHead(Q,&X)）——读取队头元素，若队列非空则用x返回队头元素

销毁队列（ClearQueue(&Q)）销毁队列，并释放队列Q占用的内存空间

存储结构

顺序存储结构

定义：采用顺序存储的队列，front——队头，rear——队尾后一个

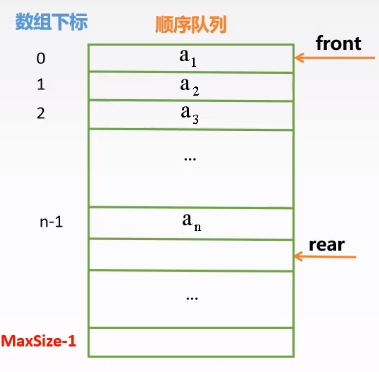
typedef struct{
    ElemType data[MaxSize];
    int front,rear;
}SqQueue;

front指向队头——rear指向队尾下一个

初始化：front、rear=0

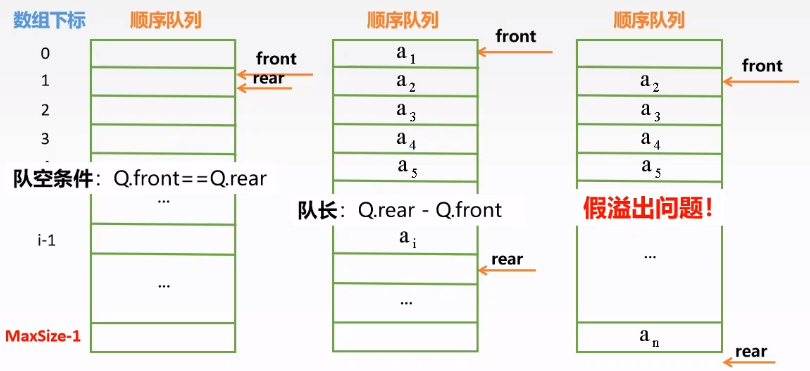
循环队列

定义：把存储队列的顺序队列在逻辑上视为一个环（将最后一个元素的后一个单元与第一个元素链接）——取余

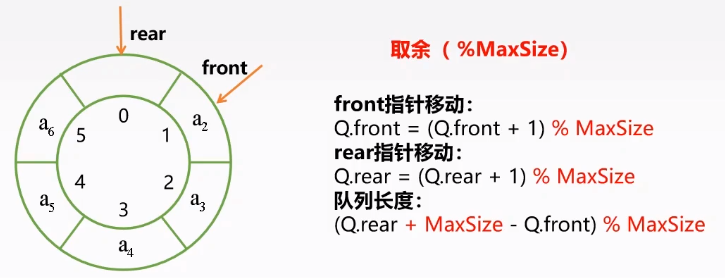
判空：Q.front==Q.rear

判满：Q.front==Q.rear

但是出现了重复！！！

方法1：牺牲一个存储单元

判空：Q.front==Q.rear

判满：Q.front==(Q.rea+1)%NaxSize

方法2：增加一个变量代表元素个数

判空：Q.size==0

判满：Q.size==MaxSize

方法3：增加tag标识

判空：Q.front==Q.rear&&tag==0

判满：Q.front==Q.rear&&tag==1

链式存储结构

定义：用链式存储的队列——带有头节点的链式队列

typedef struct{
    ElemType data;
    struct LinkNode *next;
}LinkNode;
typedef struct{
    LinkNode *front,*rear;
}LinkQueue;

初始化InitQueue(&Q)

void InitQueue(LinkQueue &Q){
    Q.front=(LinkNode*)malloc(sizrof(LinkNode));
    Q.rear=Q.front;
    Q.front->next=NULL;
}

判空isEmpty(Q)

void isEmpty(LinkQueue Q){
    if(Q.front==Q.rear)
        return true;
    else
        return false;
}

入队EnQueue(&Q, x)

尾插法

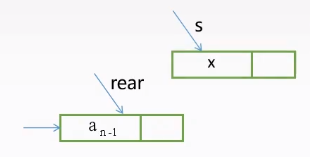
void EnQueue(LinkQueue &Q, ElemType x){
    LinkNode *s=(LinkNode*)malloc(sizeof(LinkNode));
    s->data=x;
    s->next=NULL;
    Q.rear->next=s;
    Q.rear=s;
}

出队

bool DeQueue(LinkqUEUE &Q, ElemType &x){
    if(Q.front==Q.rear)
        return false;
    LinkNode *p=Q.front->next;
    x=p->data;
    Q.front->next=p->next;
    if(Q.rear==p)			// 如果只有一个元素
        Q.rear=Q.front;
    free(p);
    return true;
}

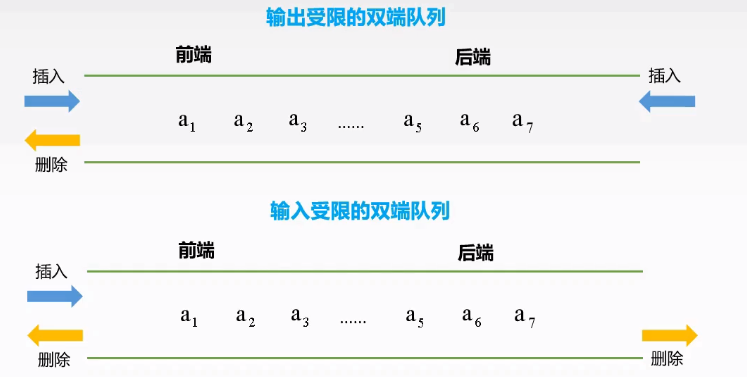
双端队列

定义：允许两端都可以进行入队和出队操作的队列

屏蔽一端的插入和删除操作，得到一个栈！！！

连续输入和输出

栈——逆序；

队列——顺序

非连续输入和输出

合法的序列：出栈序列中每一个元素后面所有比它小的元素组成一个递减序列

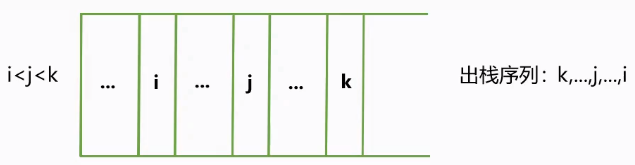
应用

栈

括号匹配

算法思想：

初始化一个空栈，顺序读入括号
若是右括号，则与栈顶元素进行匹配
1. 若匹配，则弹出栈顶元素并进行下一个元素
2. 若不匹配，则该序列不合法
若是左括号，则压入栈中
若全部元素遍历完毕，栈中非空序列不合法

表达式求值：[(A+B)*C]-[E-F]

表达式分类：

前缀表达式：+AB
中缀表达式：A+B
后缀表达式：AB+

例如：[(A+B)*C]-[E-F]

前缀表达式：+AB—>* +AB C—>* +AB C -EF—>-* +AB C -EF

后缀表达式：AB+—>AB+C*—>AB+C* EF-—>AB+C* EF—

算法思想：（中缀转后缀）

数字直接加入后缀表达式
运算符时：
1. 若为’(‘，入栈；
2. 若为’)’，则一次把栈中的运算符加入后缀表达式，直到出现’(‘，并从栈中删除’(‘;
3. 若为’+’，’-‘，’*‘，’/‘，
  1. 栈空，入栈；
  2. 栈顶元素为’(‘时，入栈；
  3. 高于栈顶元素优先级，入栈；
  4. 否则，一次弹出运算符，直到一个优先级比它低的运算符或’(‘为止；
4. 遍历完成，若栈非空依次弹出所有元素。

递归

递归表达式+递归出口

缺点：

在递归调用过程中，系统为每层返回点、局部变量、传入实参等开辟递归工作栈来进行数据存储，递归次数过多容易造成栈溢出
通常情况下递归的效率并不高

递归算法转换为非递归算法时，需要借助栈