宏定义

#define是C语言中提供的宏定义命令，它用来将一个标识符定义为一个字符串，该标识符被称为宏名，被定义的字符串称为替换文本。

该命令有两种格式：一种是简单的宏定义，另一种是带参数的宏定义。

重要：

宏替换只作替换，不做计算，不做表达式求解
宏展开不占运行时间，只占编译时间，函数调用占运行时间（分配内存、保留现场、值传递、返回值）

例题1：
1
2
3
4
5
6
7
8
#include <stdio.h>
#define N 2
#define M N+ 1
#define NUM ( M+1 )*M/2
main()
{ 
    printf( "%d\n" ,NUM ); 
}
输出结果为：$8$

解题：$NUM$——$(M+1)\cdot M/2$，$M$——$N+1$，

$NUM$=$(N+1+1)\cdot N+1/2=(N+1+1)\cdot 2+1/2=8.5$，即：$8$

例题2：
1
2
3
4
5
6
7
#define  SUM(x) 3*x*x+1
int main()
{
	int i=5,j=8;
	printf("%d\n",SUM(i+j));
	return;
}
输出结果为：$64$

解答：$SUM(i+j)=3\cdot i+j\cdot i+j+1=3\cdot 5+8\cdot 5+8+1=64$

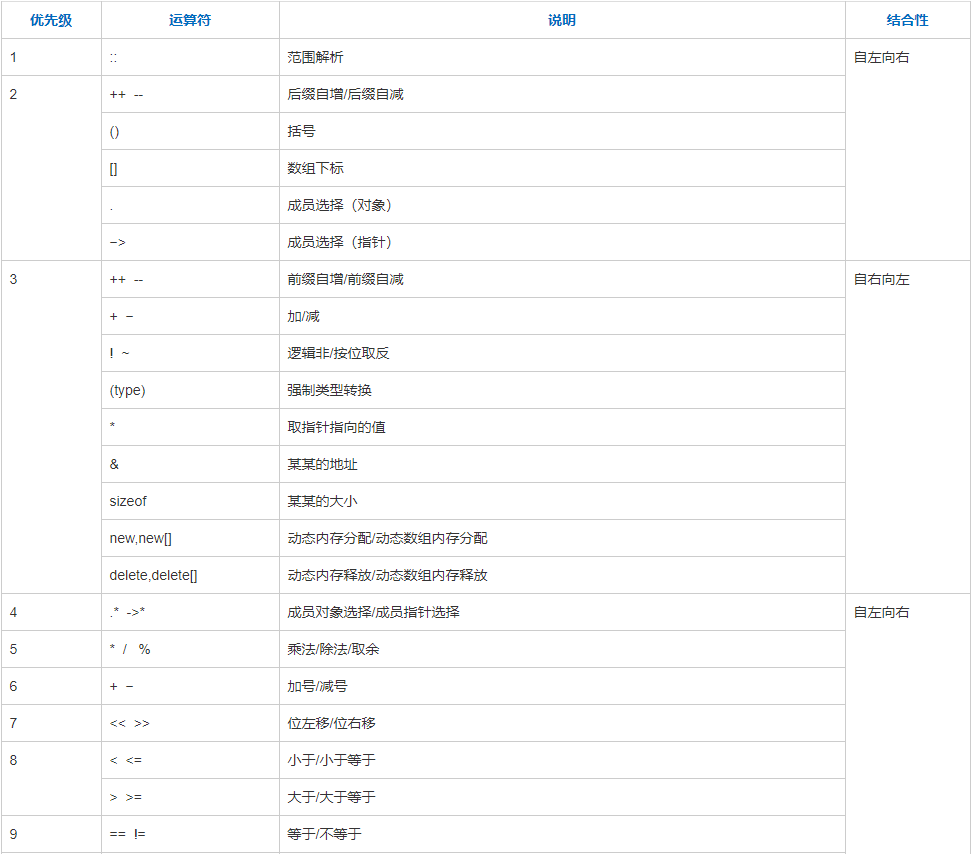
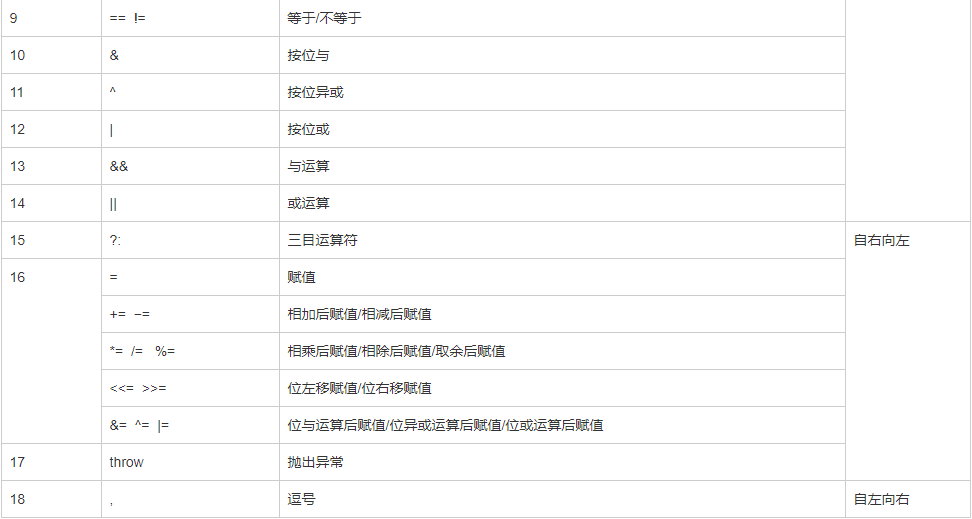
运算符

运算符是一种告诉编译器执行特定的数学或逻辑操作的符号。C++ 内置了丰富的运算符，并提供了以下类型的运算符：

算术运算符。
关系运算符。
逻辑运算符。
位运算符。
赋值运算符。
杂项运算符。

位运算符

位运算符作用于位，并逐位执行操作。&、 | 和 ^ 的真值表如下所示：

p	q	p&q	p\	q
0	0	0	0	0
0	1	0	1	1
1	1	1	1	0
1	0	0	1	1

假设如果 A = 60，且 B = 13，现在以二进制格式表示，它们如下所示：

A = 0011 1100
B = 0000 1101
-----------------
 
A&B = 0000 1100
A|B = 0011 1101
A^B = 0011 0001
~A  = 1100 0011

下表显示了 C++ 支持的位运算符。假设变量 A 的值为 60，变量 B 的值为 13，则：

运算符	描述	实例
&	如果同时存在于两个操作数中，二进制AND运算符复制一位到结果中。	(A&B)将得到12，即为0000 1100
\		如果存在于任一操作数中，二进制OR运算符复制一位到结果中。	(A\	B)将得到61，即为0011 1101
^	如果存在于其中一个操作数中但不同时存在于两个操作数中，二进制异或运算符复制一位到结果中。	(A^B)将得到49，即为0011 0001
~	二进制补码运算符是一元运算符，具有”翻转”位效果。	(~A)将得到-61，即为1100 0011，2的补码形式，带符号的二进制数。
<<	二进制左移运算符。左操作数的值向左移动右操作数指定的位数。	A<<2将得到240，即为1111 0000
>>	二进制右移运算符。左操作数的值向右移动右操作数指定的位数。	A>>2将得到15，即为0000 1111

例题1：

7&3+12的值是15 。（错误）

解答：算数运算符的优先级高于位运算。先算：$3+12=15$，$7——0111$，$15——1111$，$7\&15=0111=7$。

例题2：

如下函数，在32bits系统foo(2^31-3)的值是？
1
2
int foo (int x)
   return x & -x
结果为：$1$

解答：32位系统中，

$2^{31}=10000000,00000000,00000000,00000000$

$2^{31}-3=01111111,1111111,1111111,1111101$

$2^{31}-3=1000000,0000000,0000000,00000010$，反码

$-(2^{31}-3)=01111111，11111111，11111111，11111101$，$2^{31}-3$的反码$+1$

$-(2^{31}-3)=10000000,00000000,00000000,00000011$，补码

$2^{31}-3 \& -(2^{31}-3)=00000000,00000000,00000000,00000001=1$

反转位：

uint32_t reverseBits(uint32_t n) {
	n = (n >> 16) | (n << 16);
	n = ((n & 0xff00ff00) >> 8) | ((n & 0x00ff00ff) << 8);
	n = ((n & 0xf0f0f0f0) >> 4) | ((n & 0x0f0f0f0f) << 4);
	n = ((n & 0xcccccccc) >> 2) | ((n & 0x33333333) << 2);
	n = ((n & 0xaaaaaaaa) >> 1) | ((n & 0x55555555) << 1);
	return n;
}

0xaaaaaaaa = 10101010101010101010101010101010 (偶数位为1，奇数位为0）

0x55555555 = 1010101010101010101010101010101 (偶数位为0，奇数位为1）

0x33333333 = 110011001100110011001100110011 (1和0每隔两位交替出现)

0xcccccccc = 11001100110011001100110011001100 (0和1每隔两位交替出现)

0x0f0f0f0f = 00001111000011110000111100001111 (1和0每隔四位交替出现)

0xf0f0f0f0 = 11110000111100001111000011110000 (0和1每隔四位交替出现)

1 2	(x & 0x55555555) << 1——奇数位移到偶数位 (x >> 1) & 0x55555555)——先右移一位，等于拿到奇数位