剑指Offer——Week1

发表于 | 分类于 |
字数统计: 5.8k | 阅读时长 ≈ 23

找出数组中重复的数字

给定一个长度为 $n$的整数数组 nums，数组中所有的数字都在0~n−1​的范围内。

数组中某些数字是重复的，但不知道有几个数字重复了，也不知道每个数字重复了几次。

请找出数组中任意一个重复的数字。

注意：如果某些数字不在0~n−1​范围内，或数组中不包含重复数字，则返回-1；

样例

1
2
给定 nums = [2, 3, 5, 4, 3, 2, 6, 7]。
返回 2 或 3。

思路

  1. 首先遍历一遍数组，如果存在某个数不在0到n-1的范围内，则返回-1。
  2. 把每个数放到对应的位置上，即让nums[i] = i。

从前往后遍历数组中的所有数，假设当前遍历到的数是nums[i]=x，那么：

  • 如果x != i && nums[x] == x，则说明x出现了多次，直接返回x即可；
  • 如果nums[x] != x，那我们就把x交换到正确的位置上，即swap(nums[x], nums[i])，交换完之后如果nums[i] != i，则重复进行该操作。由于每次交换都会将一个数放在正确的位置上，所以swap操作最多会进行n次，不会发生死循环。

循环结束后，如果没有找到任何重复的数，则返回-1。

时间复杂度分析

每次swap操作都会将一个数放在正确的位置上，最后一次swap会将两个数同时放到正确位置上，一共只有n个数和n个位置，所以swap最多会进行n−1次。所以总时间复杂度是 $O(n)$。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int duplicateInArray(vector<int>& nums) {
        int n = nums.size();					        // 计算数组长度
        for(int i = 0; i < n; ++i){
            if(nums[i] < 0 || nums[i] >= n)return -1;	// 特例判断	
            while(nums[i] != i){				 // nums[i]没在正确位置
                if(nums[i] == nums[nums[i]])			// 存在重复数字
                    return nums[i];
                else
                    swap(nums[i], nums[nums[i]]);		// 交换
            }
        }  
        return -1;
    }
};

不修改数组找出重复数字

给定一个长度为n+1的数组nums，数组中所有的数均在1∼n的范围内，其中n≥1。

请找出数组中任意一个重复的数，但不能修改输入的数组。

样例

1
2
给定 nums = [2, 3, 5, 4, 3, 2, 6, 7]。
返回 2 或 3。

思考题：如果只能使用O(1)的额外空间，该怎么做呢？

思路

分治法，抽屉原理，$O(nlogn)$

抽屉原理：n+1个苹果放在n个抽屉里，那么至少有一个抽屉中会放两个苹果。

用在这个题目中就是，一共有n+1个数，每个数的取值范围是1到n，所以至少会有一个数出现两次。

将每个数的取值的区间[1, n]划分成[1, n/2]和[n/2+1, n]两个子区间，然后分别统计两个区间中数的个数。

注意这里的区间是指数的取值范围，而不是数组下标。划分之后，左右两个区间里一定至少存在一个区间，区间中数的个数大于区间长度。

因此我们可以把问题划归到左右两个子区间中的一个，而且由于区间中数的个数大于区间长度，根据抽屉原理，在这个子区间中一定存在某个数出现了两次。

依次类推，每次我们可以把区间长度缩小一半，直到区间长度为1时，我们就找到了答案。

时间复杂度分析

  1. 时间复杂度：每次会将区间长度缩小一半，一共会缩小$O(logn)$次。每次统计两个子区间中的数时需要遍历整个数组，时间复杂度是$O(n)$。所以总时间复杂度是$O(nlogn)$。
  2. 空间复杂度：代码中没有用到额外的数组，所以额外的空间复杂度是$O(1)$。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int duplicateInArray(vector<int>& nums) {
        int l = 1, r = nums.size() - 1;
        while (l < r) {
            int mid = l + r >> 1; // 划分的区间：[l, mid], [mid + 1, r]
            int s = 0;
            for (auto x : nums) s += x >= l && x <= mid;// 统计左边个数
            if (s > mid - l + 1) r = mid;
            else l = mid + 1;
        }
        return r;
    }
};

二维数组中的查找

在一个二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。

请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

样例

1
2
3
4
5
6
7
8
9
输入数组：
[
  [1,2,8,9]，
  [2,4,9,12]，
  [4,7,10,13]，
  [6,8,11,15]
]
如果输入查找数值为7，则返回true，
如果输入查找数值为5，则返回false。

思路

单调性扫描，$O(n+m)$

核心在于发现每个子矩阵右上角的数的性质：

  • 如下图所示，x左边的数都小于等于x，x下边的数都大于等于x。

因此我们可以从整个矩阵的右上角开始枚举，假设当前枚举的数是$x$：

  • 如果$x$ 等于target，则说明我们找到了目标值，返回true；
  • 如果$x$小于target，则$x$左边的数一定都小于target，我们可以直接排除当前一整行的数；
  • 如果$x$大于target，则$x$下边的数一定都大于target，我们可以直接排序当前一整列的数；

排除一整行就是让枚举的点的横坐标加一，排除一整列就是让纵坐标减一。
当我们排除完整个矩阵后仍没有找到目标值时，就说明目标值不存在，返回false。

时间复杂度分析

每一步会排除一行或者一列，矩阵一共有$n$行，$m$列，所以最多会进行$n+m$步。所以时间复杂度是$O(n+m)$。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    bool findNumberIn2DArray(vector<vector<int>>& array, int target) {
		if(array.empty() || array[0].empty()) return false;		
        int i = 0, j = array[0].size() - 1;
        while(i < array.size() && j >= 0){
            if(array[i][j] == target) return true;
            if(array[i][j] > target) --j;
            else ++i;
        }
        return false;
    }
};

替换空格

请实现一个函数，把字符串 s 中的每个空格替换成”%20“。

你可以假定输入字符串的长度最大是1000。
注意输出字符串的长度可能大于1000。

样例

1
2
输入：s = "We are happy."
输出："We%20are%20happy."

思路

线性扫描，$O(n)$

从前往后枚举原字符串：

  • 如果遇到空格，则在string类型的答案中添加 “%20“；
  • 如果遇到其他字符，则直接将它添加在答案中；

时间复杂度分析

原字符串只会被遍历常数次，所以总时间复杂度是$O(n)$。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    string replaceSpace(string s) {
		string res;
        for (auto x : s)
            if (x == ' ')
                res += "%20";
            else
                res += x;
        return res;
    }
};

从尾到头打印链表

输入一个链表的头结点，按照 从尾到头 的顺序返回节点的值。

返回的结果用数组存储。

样例

1
2
输入：[2, 3, 5]
返回：[5, 3, 2]

思路

遍历链表，$O(n)$

单链表只能从前往后遍历，不能从后往前遍历。

因此我们先从前往后遍历一遍输入的链表，将结果记录在答案数组中。
最后再将得到的数组逆序即可。

时间复杂度分析

链表和答案数组仅被遍历了常数次，所以总时间复杂度是$O(n)$。

C++代码

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    vector<int> reversePrint(ListNode* head) {
        vector<int> res;
        while (head) {
            res.push_back(head->val);
            head = head->next;
        }
        return vector<int>(res.rbegin(), res.rend());
    }
};

重建二叉树

输入一棵二叉树前序遍历和中序遍历的结果，请重建该二叉树。

注意:

  • 二叉树中每个节点的值都互不相同；
  • 输入的前序遍历和中序遍历一定合法；

样例

1
2
3
4
5
6
7
8
9
10
给定：
前序遍历是：[3, 9, 20, 15, 7]
中序遍历是：[9, 3, 15, 20, 7]
返回：[3, 9, 20, null, null, 15, 7, null, null, null, null]
返回的二叉树如下所示：
    3
   / \
  9  20
    /  \
   15   7

思路

递归，$O(n)$

递归建立整棵二叉树：先递归创建左右子树，然后创建根节点，并让指针指向两棵子树。

具体步骤如下：

  1. 先利用前序遍历找根节点：前序遍历的第一个数，就是根节点的值；
  2. 在中序遍历中找到根节点的位置k，则k左边是左子树的中序遍历，右边是右子树的中序遍历；
  3. 假设左子树的中序遍历的长度是l，则在前序遍历中，根节点后面的l个数，是左子树的前序遍历，剩下的数是右子树的前序遍历；
  4. 有了左右子树的前序遍历和中序遍历，我们可以先递归创建出左右子树，然后再创建根节点。

时间复杂度分析

我们在初始化时，用哈希表(unordered_map<int,int>)记录每个值在中序遍历中的位置，这样我们在递归到每个节点时，在中序遍历中查找根节点位置的操作，只需要$O(1)$的时间。此时，创建每个节点需要的时间是$O(1)$，所以总时间复杂度是 $O(n)$。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    map<int, int> hash;							// 开哈希表
    vector<int> preorder, inorder;				// 全局变量
    TreeNode* buildTree(vector<int>& _preorder, vector<int>& _inorder) {
        preorder = _preorder, inorder = _inorder;
        for(int  i = 0; i < inorder.size(); ++i) 
            hash[inorder[i]] = i;    			// 初始化哈希表
        return dfs(0, preorder.size() - 1, 0, inorder.size() - 1);	
    }
    TreeNode* dfs(int pl, int pr, int il, int ir){
        if(pl > pr) return nullptr;
        auto root = new TreeNode(preorder[pl]);	// 根节点
        int k = hash[root->val];			// 根节点在中序遍历中的位置
        // 前序和后序遍历的新的范围
        auto left = dfs(pl + 1, pl + k - il, il, k - 1);	
        auto right = dfs(pl + k - il +1, pr, k + 1, ir);
        root->left = left,root->right = right;
        return root;
    }
};

二叉树的下一个节点

给定一棵二叉树的其中一个节点，请找出中序遍历序列的下一个节点。

注意：

  • 如果给定的节点是中序遍历序列的最后一个，则返回空节点;
  • 二叉树一定不为空，且给定的节点一定不是空节点；

样例

1
2
3
4
5
6
假定二叉树是：[2, 1, 3, null, null, null, null]， 给出的是值等于2的节点。
则应返回值等于3的节点。
解释：该二叉树的结构如下，2的后继节点是3。
  2
 / \
1   3

思路

模拟，$O(h)$

求二叉树中给定节点的后继，分情况讨论即可，如下图所示：

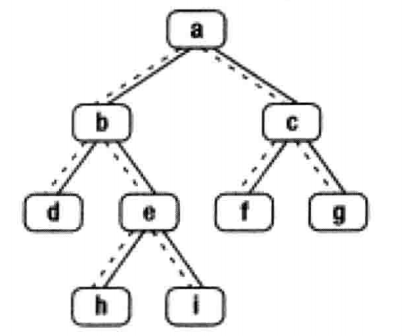
  1. 如果一个结点有右子树，那么它的下一个结点就是它的右子树的最左子结点。也就是说从右子结点出发一直沿着指向左子树结点的指针，我们就能找到它的下一个结点。例如，图中结点b的下一个结点是h，结点a的下一个结点是f。
  2. 如果结点是它父结点的左子结点，那么它的下一个结点就是它的父结点。例如，图中结点d的下一个结点是b，f的下一个结点是c。
  3. 如果一个结点既没有右子树，并且它还是父结点的右子结点，这种情形就比较复杂。 我们可以沿着指向父结点的指针一直向上遍历，直到找到一个是它父结点的左子结点的结点。如果这样的结点存在，那么这个结点的父结点就是我们要找的下一个结点。例如，为了找到结点g的下一个结点，我们沿着指向父结点的指针向上遍历，先到达结点c。由于结点c是父结点a的右结点，我们继续向上遍历到达结点a。由于结点a是树的根结点。它没有父结点。因此结点g没有下一个结点。

时间复杂度分析

不论往上找还是往下找，总共遍历的节点数都不大于树的高度。所以时间复杂度是 $O(h)$，其中h是树的高度。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    TreeNode* inorderSuccessor(TreeNode* p) {
        if(p->right){
            p = p->right;
            while(p->left) p = p->left;
            return p;
        }
        while(p->father && p == p->father->right) p = p->father;
        return p->father;
    }
};

二叉搜索树的后继

设计一个算法，找出二叉搜索树中指定节点的后继。

如果指定节点没有对应的后继，则返回null。

样例

1
2
3
4
5
6
7
8
9
输入: root = [5,3,6,2,4,null,null,1], p = 6
      5
     / \
    3   6
   / \
  2   4
 /   
1
输出: null

思路

BST+递归

首先本题中的二叉树是二叉搜索树，也就是中序遍历是单调递增的，所以我们可以利用这个性质来简化查找过程：

  • 如果结点p的值大于等于root的值，说明p的后继结点在root右子树中，那么就递归到右子树中查找。
  • 如果结点p的值小于root的值，说明p在root左子树中，而它的后继结点有两种可能，要么也在左子树中，要么就是root：
    • 如果左子树中找到了后继结点，那就直接返回答案。
    • 如果左子树中没有找到后继结点，那就说明p的右儿子为空，那么root 就是它的后继结点。

BST+非递归

  • 如果p有右儿子，那么它的后继结点就是右子树的最左边的儿子。
  • 如果p没有右儿子，那么它的后继结点就是，沿着p往上到root的路径中，第一个左儿子在路径上的结点。因为这个结点的左子树中p是最右边的结点，是最大的，所以它就是p的后继结点。因为是二叉搜索树，我们就可以从根结点开始往p走，根据结点值的大小决定走的方向。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/* 递归*/
class Solution {
public:
    TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
        if(root = NULL || p == NULL) return NULL;
        if(p->val >= root->val){
            return inorderSuccessor(root->right, p);
        } else {
            TreeNode* left = inorderSuccessor(root->left, p);
            return left ? left : root;
        }
    }
};
/* 非递归*/
class Solution {
public:
    TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
        if (p->right) {
            p = p->right;
            while (p->left) p = p->left;
            return p;
        }
        TreeNode* res = NULL;
        while (root != p) {
            if (root->val < p->val) {		// 根据大小判断走向
                root = root->right;
            } else {
                res = root;
                root = root->left;
            }
        }
        return res;
    }
};

用两个栈实现队列

请用栈实现一个队列，支持如下四种操作：

  • push(x) – 将元素x插到队尾；
  • pop() – 将队首的元素弹出，并返回该元素；
  • peek() – 返回队首元素；
  • empty() – 返回队列是否为空；

样例

1
2
3
4
MyQueue queue = new MyQueue();
queue.push(1);
queue.push(2);
queue.pop();

思路

栈，队列，$O(n)$

我们用两个栈来做，一个主栈，用来存储数据；一个辅助栈，用来当缓存。

  • push(x)，我们直接将x插入主栈中即可。
  • pop()，此时我们需要弹出最先进入栈的元素，也就是栈底元素。我们可以先将所有元素从主栈中弹出，压入辅助栈中。则辅助栈的栈顶元素就是我们要弹出的元素，将其弹出即可。然后再将辅助栈中的元素全部弹出，压入主栈中。
  • peek()，可以用和pop()操作类似的方式，得到最先压入栈的元素。
  • empty()，直接判断主栈是否为空即可。

时间复杂度分析

  • push()：$O(1)$；
  • pop(): 每次需要将主栈元素全部弹出，再压入，所以需要$O(n)$的时间；
  • peek()：类似于pop()，需要$O(n)$的时间；
  • empty()：$O(1)$；

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class CQueue {
    stack<int> stack1,stack2;
public:
    CQueue() {
        while (!stack1.empty()) {
            stack1.pop();
        }
        while (!stack2.empty()) {
            stack2.pop();
        }
    }
    
    void appendTail(int value) {
        stack1.push(value);
    }
    
    int deleteHead() {
        // 如果第二个栈为空
        if (stack2.empty()) {
            while (!stack1.empty()) {
                stack2.push(stack1.top());
                stack1.pop();
            }
        } 
        if (stack2.empty()) {
            return -1;
        } else {
            int deleteItem = stack2.top();
            stack2.pop();
            return deleteItem;
        }
    }
};

斐波那契数列

输入一个整数n，求斐波那契数列的第n项。

假定从0开始，第0项为0。(n<=39)

样例

1
2
输入整数 n=5 
返回 5

思路

递归，$O(n)$

用两个变量滚动式得往后计算，a表示第n−1项，b表示第n项。
则令c=a+b表示第n+1项，然后让a,b顺次往后移一位。

时间复杂度分析

总共需要计算n次，所以时间复杂度是O(n)。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int fib(int n) {
        // 动态规划5行解决
        // 声明n+1+1大小的vector（第一个+1是要存储0至n共n+1个数据；第二个+1是考虑n==0的情况，保证v[1]不越界）
        vector<int> v(n + 1 + 1, 0); 
        v[1] = 1;
        for(int i = 2; i <= n; i++)
            v[i] = (v[i - 1] + v[i - 2]) % 1000000007; //注意别忘记取余
        return v[n];                     //直接返回最后一个数，即最终结果
    }
};

旋转数组的最小数字

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。

输入一个升序的数组的一个旋转，输出旋转数组的最小元素，即寻找 右排序数组 的首个元素 numbers[x] ，称x为 旋转点 。

例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转，该数组的最小值为1。数组可能包含重复项。

注意：数组内所含元素非负，若数组大小为0，请返回-1。

样例

1
2
输入：nums=[2,2,2,0,1]
输出：0

思路

二分，$O(n)$

为了便于分析，我们先将数组中的数画在二维坐标系中，横坐标表示数组下标，纵坐标表示数值，如下所示：

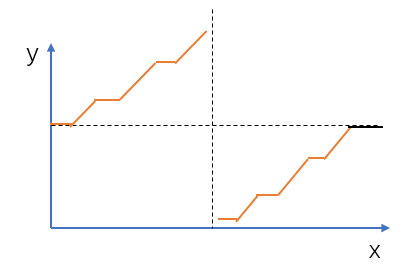
图中水平的实线段表示相同元素。我们发现除了最后水平的一段（黑色水平那段）之外，其余部分满足二分性质：竖直虚线左边的数满足nums[i]≥nums[0]；而竖直虚线右边的数不满足这个条件。
分界点就是整个数组的最小值。所以我们先将最后水平的一段删除即可。

另外，不要忘记处理数组完全单调的特殊情况：

  • 当我们删除最后水平的一段之后，如果剩下的最后一个数大于等于第一个数，则说明数组完全单调。

  1. 循环二分： 设置i, j 指针分别指向 numbers数组左右两端，m = (i + j) // 2为每次二分的中点（ “//“ 代表向下取整除法，因此恒有$i \leq m < j$），可分为以下三种情况：

    1. 当numbers[m] > numbers[j]时：m一定在左排序数组中，即旋转点x一定在 [m + 1, j]闭区间内，因此执行i = m + 1；
    2. 当numbers[m] < numbers[j]时：m一定在 右排序数组中，即旋转点x一定在[i, m] 闭区间内，因此执行j = m；
    3. 当numbers[m] == numbers[j]时： 无法判断m在哪个排序数组中，即无法判断旋转点x在[i, m]还是[m + 1, j]区间中。解决方案： 执行j = j - 1缩小判断范围 （分析见以下内容） 。

  2. 返回值： 当i = j时跳出二分循环，并返回numbers[i]即可。

时间复杂度分析

二分的时间复杂度是O(logn)，删除最后水平一段的时间复杂度最坏是O(n)，所以总时间复杂度是O(n)。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int minArray(vector<int>& numbers) {
		int n = nums.size() - 1;
        if(n < 0) return -1;
        while(n > 0 && nums[n] == nums[0]) --n;	    // 处理最后一段水平相等的元素
        if(nums[n] >= nums[0]) return nums[0];		// 判断第二部分是否存在
        int l = 0, r = n;				// 开始二分
        while(l < r){
            int mid = l + r >> 1;		// [l, mid], [mid + 1, r]
            if(nums[mid] < nums[0]) r = mid;
            else l = mid + 1;
        }
        return nums[r];
    }
};

矩阵中的路径

请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。

路径可以从矩阵中的任意一个格子开始，每一步可以在矩阵中向左，向右，向上，向下移动一个格子。

如果一条路径经过了矩阵中的某一个格子，则之后不能再次进入这个格子。

注意：

  • 输入的路径不为空；
  • 所有出现的字符均为大写英文字母；

样例

1
2
3
4
5
6
7
8
matrix=
[
  ["A","B","C","E"],
  ["S","F","C","S"],
  ["A","D","E","E"]
]
str="BCCE" , return "true" 
str="ASAE" , return "false"

思路

DFS，$O(n^23^k)$

在深度优先搜索中，最重要的就是考虑好搜索顺序。

我们先枚举单词的起点，然后依次枚举单词的每个字母。
过程中需要将已经使用过的字母改成一个特殊字母，以避免重复使用字符。

时间复杂度分析

单词起点一共有$n^2$ 个，单词的每个字母一共有上下左右四个方向可以选择，但由于不能走回头路，所以除了单词首字母外，仅有三种选择。所以总时间复杂度是$O(n^23^k)$。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    bool exist(vector<vector<char>>& board, string word) {
		for (int i = 0; i < board.size(); i ++ )
            for (int j = 0; j < board[i].size(); j ++ )
                if (dfs(board, word, 0, i, j))
                    return true;
        return false;
    }

    bool dfs(vector<vector<char>> &board, string &word, int u, int x, int y) {
        if (board[x][y] != word[u]) return false;
        if (u == word.size() - 1) return true;
        int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
        char t = board[x][y];
        board[x][y] = '*';
        for (int i = 0; i < 4; i ++ ) {
            int a = x + dx[i], b = y + dy[i];
            if (a >= 0 && a < board.size() && b >= 0 && b < board[a].size()) {
                if (dfs(board, word, u + 1, a, b)) return true;
            }
        }
        board[x][y] = t;
        return false;
    }
};

二分查找模板

二分模板一共有两个，分别适用于不同情况。
算法思路：假设目标值在闭区间[l, r]中， 每次将区间长度缩小一半，当l = r时，我们就找到了目标值。

版本1

当我们将区间[l, r]划分成[l, mid]和[mid + 1, r]时，其更新操作是r = mid或者l = mid + 1;，计算mid时不需要加1。

C++ 代码模板：

1
2
3
4
5
6
7
8
9
10
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;
        else l = mid + 1;
    }
    return l;
}

版本2

当我们将区间[l, r]划分成[l, mid - 1]和[mid, r]时，其更新操作是r = mid - 1或者l = mid;，此时为了防止死循环，计算mid时需要加1。

C++ 代码模板：

1
2
3
4
5
6
7
8
9
10
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}
-------------本文结束 感谢您的阅读-------------

本文标题:剑指Offer——Week1

文章作者:善雯

发布时间:2020年07月09日 - 11:07

最后更新:2020年07月15日 - 20:07

原始链接:http://shanwenyang.github.io/2020/07/09/Offer-Week1/

许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。

原创技术分享，您的支持将鼓励我继续创作
0%