剑指Offer——Week2

发表于 | 分类于 |
字数统计: 6k | 阅读时长 ≈ 25

机器人的运动范围

地上有一个m行和n列的方格，横纵坐标范围分别是0∼m−1和 0∼n−1。一个机器人从坐标[0,0]的格子开始移动，每一次只能向左，右，上，下四个方向移动一格。但是不能进入行坐标和列坐标的数位之和大于k的格子。请问该机器人能够达到多少个格子？

样例

1
2
输入：k=7, m=4, n=5
输出：20

样例2

1
2
3
4
输入：k=18, m=40, n=40
输出：1484
解释：当k为18时，机器人能够进入方格（35,37），因为3+5+3+7 = 18。
      但是，它不能进入方格（35,38），因为3+5+3+8 = 19。

注意:

  1. 0<=m<=50
  2. 0<=n<=50
  3. 0<=k<=100

思路

BFS，$O(nm)$

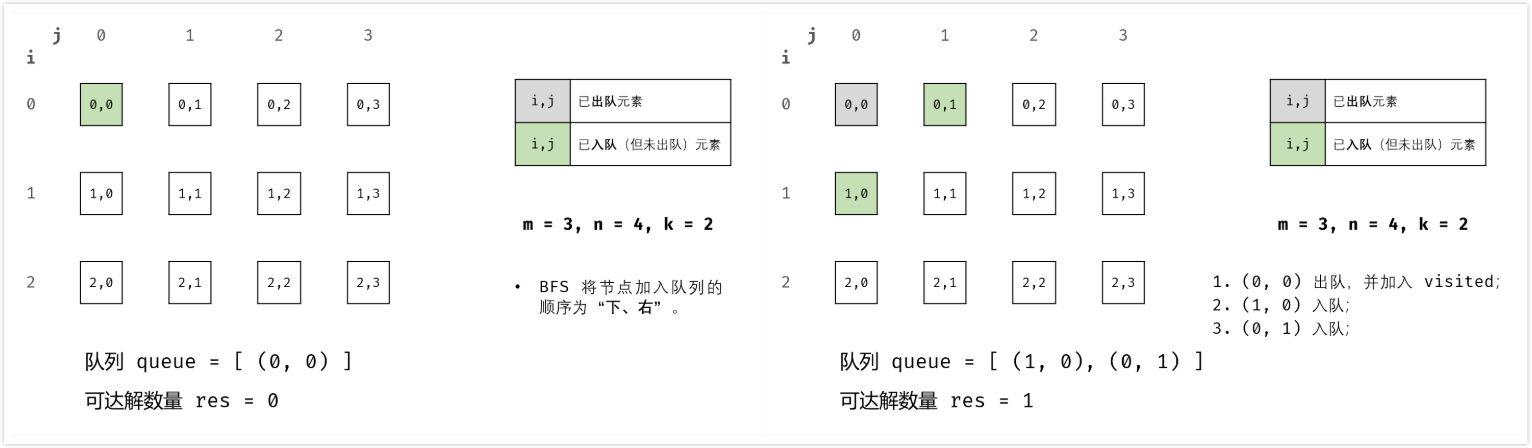
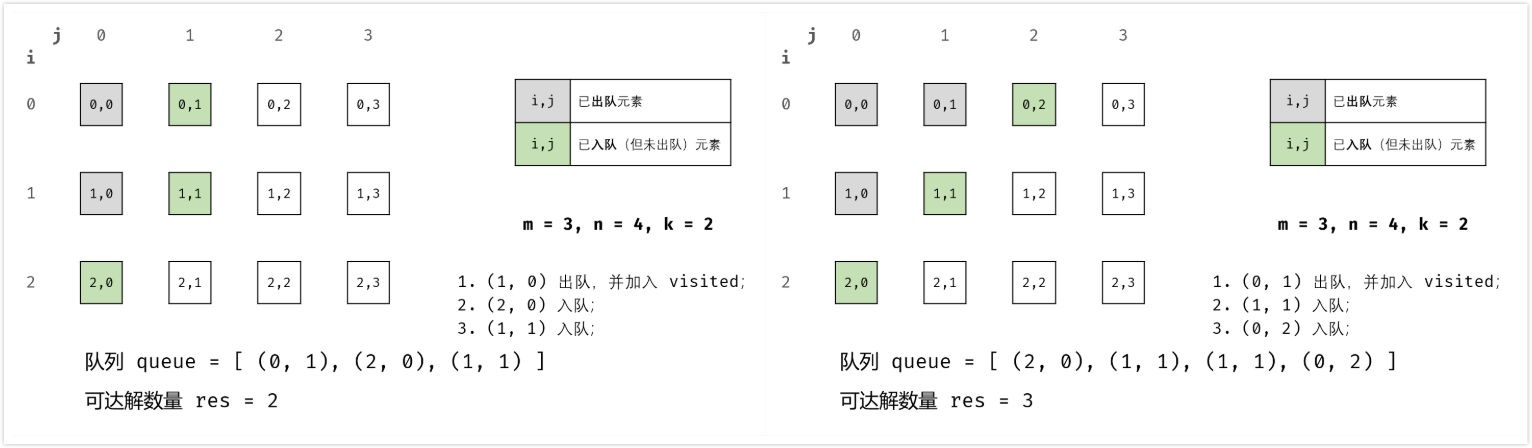
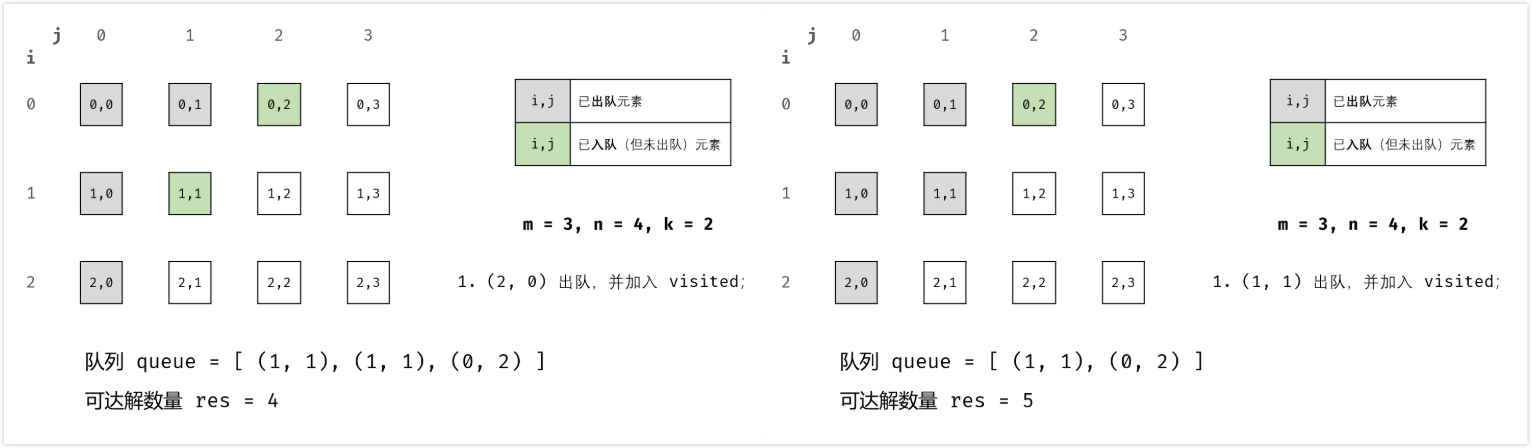
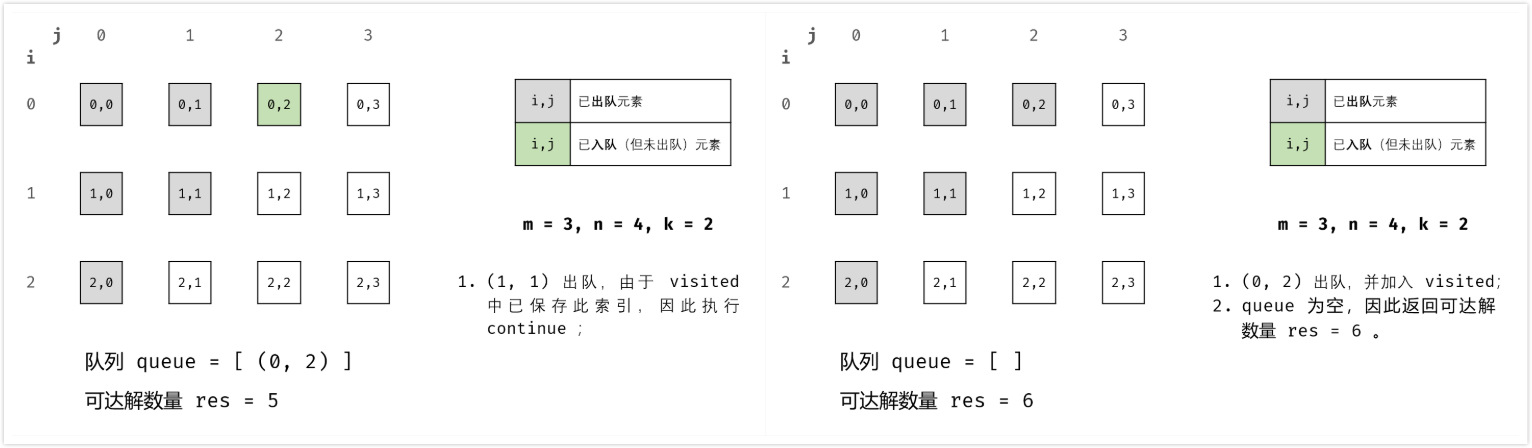
这是一个典型的宽度优先搜索问题，我们从 (0, 0) 点开始，每次朝上下左右四个方向扩展新的节点即可。

扩展时需要注意新的节点需要满足如下条件：

  • 之前没有遍历过，这个可以用个bool数组来判断；
  • 没有走出边界；
  • 横纵坐标的各位数字之和小于k；

最后答案就是所有遍历过的合法的节点个数。

时间复杂度分析

每个节点最多只会入队一次，所以时间复杂度不会超过方格中的节点个数。
最坏情况下会遍历方格中的所有点，所以时间复杂度就是$O(nm)$。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
    int get(int x) {				// 计算 x 的数位之和
        int res = 0;
        for (; x; x /= 10) {
            res += x % 10;
        }
        return res;
    }
public:
    int movingCount(int m, int n, int k) {
        if (!k) return 1;
        queue<pair<int,int> > Q;		// 建立搜索队列
        int dx[2] = {0, 1};				// 向右和向下的方向数组
        int dy[2] = {1, 0};
        vector<vector<int> > vis(m, vector<int>(n, 0)); // 遍历状态数组
        Q.push({0, 0});					// 加入起点
        vis[0][0] = 1;					// 起点状态为1
        int ans = 1;					// 答案+1
        while (!Q.empty()) {
            auto [x, y] = Q.front();		// 队首元素
            Q.pop();						// 弹出
            for (int i = 0; i < 2; ++i) {
                int tx = dx[i] + x;
                int ty = dy[i] + y;
                if (tx < 0 || tx >= m || ty < 0 || ty >= n || vis[tx][ty] || get(tx) + get(ty) > k) continue;		 // 大于阈值条件继续
                Q.push({x, ty});				// 满足条件加入队列 
                vis[tx][ty] = 1;				// 遍历状态
                ans++;							// 答案加1
            }
        }
        return ans;
    }
};

剪绳子——整数划分

给你一根长度为$n$绳子，请把绳子剪成$m$段（$m$、$n$都是整数，$2≤n≤58$并且$m≥2$）。每段的绳子的长度记为$k[0]$、$k[1]$、……、$k[m]$。$k[0]$、$k[1]$、…、$k[m]$可能的最大乘积是多少？例如当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到最大的乘积18。

样例

1
2
输入：8
输出：18

思路

数学，$O(n)$

这道题目是数学中一个很经典的问题。
下面我们给出证明：

首先把一个正整数$N$拆分成若干正整数只有有限种拆法，所以存在最大乘积。

  1. 当$n \leq 3$时，按照规则应不切分，但由于题目要求必须剪成 $m>1$段，因此必须剪出一段长度为$1$的绳子，即返回$1 \times (n−1)$。
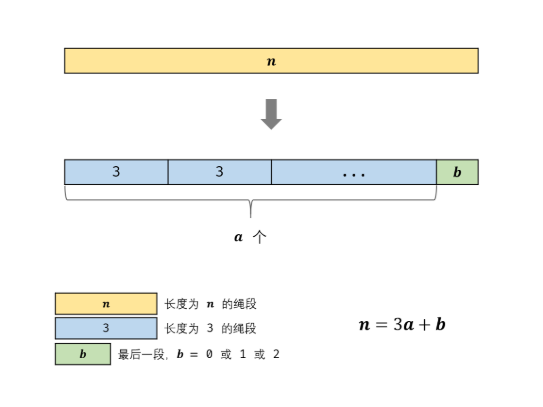
  2. 当$n>3$时，求$n$除以$3$的整数部分$a$和余数部分$b$（即$n = 3a + b$），并分为以下三种情况：
    • 当$b=0$时，直接返回$3^a$；
    • 当$b=1$时，要将一个$1 + 3$转换为$2+2$，因此返回$3^{a-1}\times4$；
    • 当$b = 2$时，返回$3^a \times 2$。

综上，选用尽量多的3，直到剩下2或者4时，用2。

时间复杂度分析

当$n$比较大时，$n$会被拆分成$⌈n/3⌉$个数，我们需要计算这么多次减法和乘法，所以时间复杂度是 $O(n)$。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
/*
n > 0, n = n1 + n2 + ... + nk
*/
class Solution {
public:
    int cuttingRope(int n) {
        if (n <= 3) return 1 * (n - 1);
        int a = n / 3, b = n % 3;
        if(b ==0) return pow(3, a);				// 情况1
        if(b == 1) return pow(3, a - 1) * 4;	// 情况2
        return pow(3, a) * 2;					// 情况3
    }
};

二进制中1的个数

输入一个32位整数，输出该数二进制表示中1的个数。

注意：

  • 负数在计算机中用其绝对值的补码来表示。

样例1

1
2
3
输入：9
输出：2
解释：9的二进制表示是1001，一共有2个1。

样例2

1
2
3
4
输入：-2
输出：31
解释：-2在计算机里会被表示成11111111111111111111111111111110，
      一共有31个1。

思路

位运算，$O(logn)$

迭代进行如下两步，直到$n$变成$0$为止：

  1. 如果$n$在二进制表示下末尾是$1$，则在答案中加$1$；
  2. 将$n$右移一位，也就是将$n$在二进制表示下的最后一位删掉；

这里有个难点是如何处理负数。在C++中如果我们右移一个负整数，系统会自动在最高位补$1$，这样会导致$n$永远不为$0$，就死循环了。
解决办法是把$n$强制转化成无符号整型，这样$n$的二进制表示不会发生改变，但在右移时系统会自动在最高位补$0$。

$n\&(n-1)$

  • $(n-1)$： 二进制数字n最右边的1变成0，此1右边的0都变成1。
  • $n\&(n-1)$： 二进制数字n最右边的1变成0，其余不变。

时间复杂度分析

每次会将$n$除以$2$，最多会除$logn$次，所以时间复杂度是$O(logn)$。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/*有符号*/
class Solution {
public:
    int hammingWeight(uint32_t _n) {
        unsigned int n = _n;  					// 转化为无符号整数，表示一样，解释含义不一样
        int s = 0;
        while(n) s += n & 1, n >>= 1;
        return s;
    }
}; 
/*无符号*/
class Solution {
public:
    int hammingWeight(uint32_t n) {
        int res = 0;
        while(n) res += n & 1, n >>= 1; 
        return res;
    }
};
/* n&(n-1)*/
class Solution {
public:
    int hammingWeight(uint32_t n) {
        int res = 0;
        while(n != 0) {
            res++;
            n &= n - 1;
        }
        return res;
    }
};

数值的整数次方

实现函数double Power(double base, int exponent)，求base的 exponent次方。不得使用库函数，同时不需要考虑大数问题。

注意：

  • 不会出现底数和指数同为0的情况
  • 当底数为0时，指数一定为正

样例1

1
2
输入：10 ，2
输出：100

样例2

1
2
输入：10 ，-2  
输出：0.01

思路

快速幂，$O(n)$

求 $x^n$ 最简单的方法是通过循环将$n$个$x$乘起来，依次求$x^1$, $x^2$, …, $x^{n-1}$, $x^n$，时间复杂度为$O(n)$。快速幂法可将时间复杂度降低至$O(log_2n)$，

快速幂（二进制）

利用十进制数字$n$的二进制表示，可对快速幂进行数学化解释。

  • 对于任何一个十进制正整数$n$，设其二进制为”$b_m…b_3b_2n_1$“（$b_i$为二进制某位的值，$i\in[1,m]$），则有：
    • 二进制转十进制： $n=1b_1+2b_2+4b_3+…+n^{m-1}b_m$（ 即二进制转十进制公式 ）
    • 幂的二进制展开 ：$x^n=x^{1b_1+2b_2+4b_3+…+n^{m-1}b_m}=x^{1b_1}x{2b_2}x^{4b_3}…x^{2^{m-1}b_m}$
  • 根据以上推导，可把$x^{n}$转化为以下两个问题：
    • 计算$x^1,x^2,x^4,…,x^{2^{m-1}}$的值：循环赋值操作$x=x^2$即可；
    • 获取二进制的各位$b_1,b_2,b_3,…,b_m$的值：循环执行一下操作：
      • n&1（与操作）：判断$n$二进制中最右边是否为1；
      • n>>1（移位操作）：$n$右移一位；
  • 因此，应用以上操作，可在循环中依次计算$x^{2^0b_1},x{2^1b_2}x^{2^2b_3}…x^{2^{m-1}b_m}$的值，并将所有的$x^{2^{i-1}b_i}$累积相乘即可。
    • 当$b_i=0$时：$x^{2^{i-1}b_i}=1$；
    • $b_i=1$时：$x^{2^{i-1}b_i}=x^{2^{i-1}}$；

快速幂（二分法）

快速幂实际上是二分思想的一种应用。

  • 二分推导：$x^n=x^{n/2}\times x^{n/2}=(x^2)^{n/2}$，令$n/2$为整数，则需要分为奇数和偶数两种情况（设向下取整符号为“//”）：
    • 当$n$为偶数：$x^n=(x^2)^{n//2}$
    • 当$n$为奇数：$x^n=(x^2)^{n//2}$，即会多出一项$x$
  • 幂结果获取：
    • 根据二分推导，可通过循环 $x=x^2$操作，每次把幂从$n$降至$n//2$，直到将幂将为$0$
    • 设$res=1$，则初始状态$x^n=x^n\times res$，则循环二分时，每当$n$为奇数时，将多出的一项$x$乘以$res$，则最终可化为$x^n=x^0\times res=res$，返回$res$即可

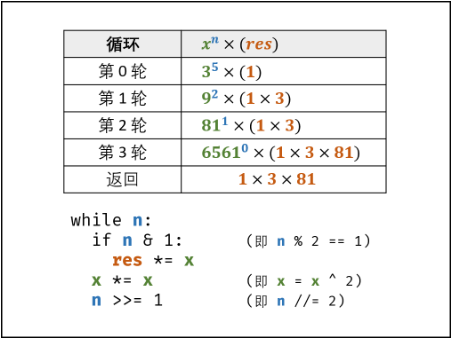
  • 转化为位运算：
    • 向下整除$n//2$等价于右移一位$n>>1$；
    • 取余数$n\%2$等价于判断二进制最右一位值$n\&1$；

算法流程：

  1. 当$x=0$时，直接返回$0$（避免后续$x=1/x$操作报错）
  2. 初始化$res=1$
  3. 当$n<0$时：把问题转化为$n>=0$的范围内，即执行$x=1/x$，$n=-n$；
  4. 循环计算：当$x=0$时跳出：
    1. 当$n\&1=1$时：将当前$x$乘入$res$（即$res*=x$）
    2. 执行$x=x^2$（即$x*=x$）
    3. 执行$n$右移一位（即$n>>=1$）
  5. 返回$res$

时间复杂度分析

假设指数是$n$，则一共会循环$O(logn)$次，所以时间复杂度是$O(logn)$。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    double myPow(double x, int n) {
        if(x == 0) return 0;		// 1.
        long b = n;					// 将n转化为长整型
        double res = 1.0;			// 2.
        if(b < 0){					// 3.
            x = 1 / x;
            b = -b;
        }
        while(b > 0){				// 4.
            if((b & 1) == 1) res *= x;	// 4.1
            x *= x;						// 4.2
            b >>= 1;					// 4.3
        }
        return res;						// 5.
    }
};

在$O(1)$时间删除链表结点

给定单向链表的一个节点指针，定义一个函数在$O(1)$时间删除该结点。

假设链表一定存在，并且该节点一定不是尾节点。

样例

1
2
3
输入：链表 1->4->6->8
删掉节点：第2个节点即6（头节点为第0个节点）
输出：新链表 1->4->8

思路

链表，$O(1)$

由于是单链表，我们不能找到前驱节点，所以我们不能按常规方法将该节点删除。我们可以换一种思路，将下一个节点的值复制到当前节点，然后将下一个节点删除即可。

时间复杂度分析

只有常数次操作，所以时间复杂度$O(1)$。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    ListNode* deleteNode(ListNode* head, int val) {
        if(head==NULL) return NULL;
        else if(head->val==val) return head->next;
        else{
            ListNode* p = head;
            while(p->next != NULL)
            {
                auto q = p->next;
                if((p->next)->val==val)
                {
                    p->next=q->next;
                    delete q;
                    break;
                }
                else
                    p=p->next;
            }
            return head;
        }
    }
};

删除排序链表中重复的结点

在一个排序的链表中，存在重复的结点，请删除该链表中重复的结点，重复的结点不保留。

样例1

1
2
输入：1->2->3->3->4->4->5
输出：1->2->5

思路

线性扫描，O(n)

为了方便处理边界情况，我们定义一个虚拟元素dummy指向链表头节点。然后从前往后扫描整个链表，每次扫描元素相同的一段，如果这段中的元素个数多于1个，则将整段元素直接删除。

时间复杂度分析

整个链表只扫描一遍，所以时间复杂度是$O(n)$。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/* 凡是头结点可能会被删掉的，定义虚拟头结点*/
class Solution {
public:
    ListNode* deleteDuplicates(ListNode* head) {
        auto dummy = new ListNode(-1);
        dummy->next = head;
        auto p = dummy;
        while (p->next) {
            auto q = p->next;
            while (q && p->next->val == q->val) q = q->next;

            if (p->next->next == q) p = p->next;
            else p->next = q;
        }
        return dummy->next;
    }
};

正则表达式匹配

请实现一个函数用来匹配包含’. ‘和’*‘的正则表达式。模式中的字符’.‘表示任意一个字符，而’*‘表示它前面的字符可以出现任意次（含0次）。在本题中，匹配是指字符串的所有字符匹配整个模式。例如，字符串”aaa“与模式”a.a“和”ab*ac*a“匹配，但与”aa.a“和”ab*a“均不匹配。

样例

1
2
3
4
5
输入：
s = "aa"
p = "a"
输出：false
解释："a" 无法匹配 "aa" 整个字符串。

思路

动态规划，$O(nm)$

状态表示：f[i][j]​表示s[i,...]​和p[j,...]相匹配
状态转移：

  1. p[i]是正常字符串,f[i][j]=s[i]==p[j]&&f[i+1][j+1];
  2. p[j]是’.‘,f[i][j]=f[i+1][j+1];
  3. p[j+1]是’*‘,f[i][j]=f[i][j+2] || f[i+1][j]

时间复杂度分析

$n$表示$s$的长度，$m$表示$p$的长度，总共$nm$个状态，状态转移复杂度 $O(1)$，所以总时间复杂度是$O(nm)$.

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    vector<vector<int>>f;
    int n, m;
    bool isMatch(string s, string p) {
        n = s.size();
        m = p.size();
        f = vector<vector<int>>(n + 1, vector<int>(m + 1, -1));
        return dp(0, 0, s, p);
    }

    bool dp(int x, int y, string &s, string &p)
    {
        if (f[x][y] != -1) return f[x][y];
        if (y == m)
            return f[x][y] = x == n;
        bool first_match = x < n && (s[x] == p[y] || p[y] == '.');
        bool ans;
        if (y + 1 < m && p[y + 1] == '*')
        {
            ans = dp(x, y + 2, s, p) || first_match && dp(x + 1, y, s, p);
        }
        else
            ans = first_match && dp(x + 1, y + 1, s, p);
        return f[x][y] = ans;
    }
};

表示数值的字符串

请实现一个函数用来判断字符串是否表示数值（包括整数和小数）。

例如，字符串"+100","5e2","-123","3.1416"和"-1E-16"都表示数值。

但是"12e","1a3.14","1.2.3","+-5"和"12e+4.3"都不是。

注意:

  1. 小数可以没有整数部分，例如.123等于0.123；
  2. 小数点后面可以没有数字，例如233.等于233.0；
  3. 小数点前面和后面可以有数字，例如233.666
  4. 当e或E前面没有数字时，整个字符串不能表示数字，例如.e1、e1；
  5. 当e或E后面没有整数时，整个字符串不能表示数字，例如12e、12e+5.4;

样例：

1
2
输入: "0"
输出: true

思路

模拟，字符串处理，$O(n)$

  1. 先去除行首和行尾空格；
  2. 行首如果有一个正负号，直接忽略；
  3. 如果字符串为空或只有一个'.'，则不是一个合法数；
  4. 循环整个字符串，去掉一下几种情况：
    1. '.'或'e'多于1个
    2. '.'在'e'后面出现
    3. 'e'后面或前面为空，或者'e'前面紧跟'.'
    4. 'e'后面紧跟正负号，但正负号后面为空

有限状态自动机

字符类型： 空格 「`」、数字「0—9」 、正负号 「+-」 、小数点 「.」 、幂符号 「e`」 。

状态定义： 按照字符串从左到右的顺序，定义以下 9 种状态：

  1. 开始的空格
  2. 幂符号前的正负号
  3. 小数点前的数字
  4. 小数点、小数点后的数字
  5. 当小数点前为空格时，小数点、小数点后的数字
  6. 幂符号
  7. 幂符号后的正负号
  8. 幂符号后的数字
  9. 结尾的空格

结束状态：合法状态为2、3、7、8

算法流程：

  1. 初始化：
    1. 状态转移表$states$： 设$states[i]$，其中$i$为所处状态， $states[i]$使用哈希表存储可转移至的状态。键值对 $(key, value)$含义：若输入$key$，则可从状态$i$转移至状态$value$。
    2. 当前状态$p$： 起始状态初始化为$p=0$。
  2. 状态转移循环：遍历字符串$s$的每个字符$c$：
    1. 记录字符类型$t$： 分为四种情况。
      • 当$c$为正负号时，执行t = 's';
      • 当$c$为数字时，执行t = 'd';
      • 当$c$为.,e,E, 空格时，执行t = c（即用字符本身表示字符类型）;
      • 否则，执行t = '?'，代表为不属于判断范围的非法字符，后续直接返回false。
    2. 终止条件： 若字符类型t不在哈希表$states[p]$中，说明无法转移至下一状态，因此直接返回false`。
    3. 状态转移： 状态$p$转移至$states[p][t]$ 。
  3. 返回值： 跳出循环后，若状态$p \in {2, 3, 7, 8}$，说明结尾合法，返回true，否则返回false。

时间复杂度

整个字符串值遍历一遍，所以时间复杂度是$O(n)$

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
public:
    bool isNumber(string s) {
		int i = 0;
        while (i < s.size() && s[i] == ' ') i ++ ;  		// 删除前面空格
        int j = s.size() - 1;
        while (j >= 0 && s[j] == ' ') j -- ;        		// 删除后面空格
        if (i > j) return false;
        s = s.substr(i, j - i + 1);

        if (s[0] == '-' || s[0] == '+') s = s.substr(1);
        if (s.empty() || s[0] == '.' && s.size() == 1) return false;    // // +,-,.

        int dot = 0, e = 0;
        for (int i = 0; i < s.size(); i ++ )
        {
            if (s[i] >= '0' && s[i] <= '9');
            else if (s[i] == '.')
            {
                dot ++ ;
                if (e || dot > 1) return false;      		// 2323.2323.23,232e.232
            }
            else if (s[i] == 'e' || s[i] == 'E')
            {
                e ++ ;
                if (i + 1 == s.size() || !i || e > 1 || i == 1 && s[0] == '.') 
                    return false; 							// e121212,2323e,1212e1212e
                if (s[i + 1] == '+' || s[i + 1] == '-')
                {
                    if (i + 2 == s.size()) return false;    // 1212e+
                    i ++ ;
                }
            }
            else return false;
        }
        return true;
    }
};

调整数组顺序使奇数位于偶数前面

输入一个整数数组，实现一个函数来调整该数组中数字的顺序。使得所有的奇数位于数组的前半部分，所有的偶数位于数组的后半部分。

样例

1
2
输入：[1,2,3,4,5]
输出: [1,3,5,2,4]

思路

双指针扫描，$O(n)$

用两个指针分别从首尾开始，往中间扫描。扫描时保证第一个指针前面的数都是奇数，第二个指针后面的数都是偶数。

  1. 初始化：i,j双指针，分别指向数组nums左右两端；
  2. 循环交换： 当i=j时跳出；
    1. 指针i遇到奇数则执行i=i+1跳过，直到找到偶数；
    2. 指针j遇到偶数则执行j=j−1跳过，直到找到奇数；
    3. 交换nums[i]和nums[j]值；
  3. 返回值： 返回已修改的nums数组。

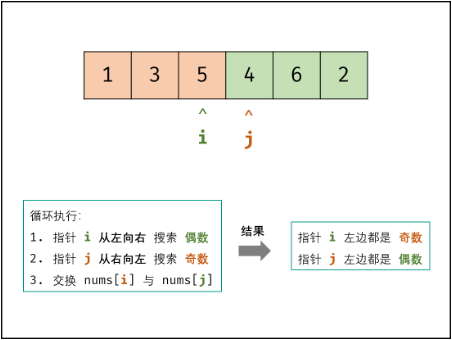
可始终保证： 指针i左边都是奇数，指针j右边都是偶数 。

时间复杂度分析

当两个指针相遇时，走过的总路程长度是$n$，所以时间复杂度是$O(n)$。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    vector<int> exchange(vector<int>& array) {
        int l = 0, r = array.size() - 1;
         while (l < r) {
             while (l < r && array[l] % 2 == 1) l ++ ;
             while (l < r && array[r] % 2 == 0) r -- ;
             if (l < r) swap(array[l], array[r]);
         }
         return array;
    }
};

链表中倒数第k个结点

输入一个链表，输出该链表中倒数第k个结点。

注意：

  • k >= 0;
  • 如果k大于链表长度，则返回 NULL;

样例

1
2
输入：链表：1->2->3->4->5 ，k=2
输出：4

思路

链表，$O(n)$

由于单链表不能索引到前驱节点，所以只能从前往后遍历。

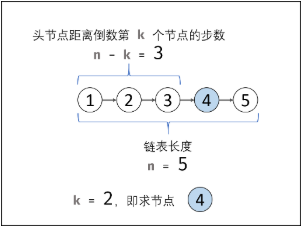
  1. 先遍历统计链表长度，记为n ；
  2. 设置一个指针走(n−k)步，即可找到链表倒数第k个节点。

双指针法：

算法流程：

  1. 初始化： 前指针former、后指针latter，双指针都指向头节点head。
  2. 构建双指针距离： 前指针former先向前走k步（结束后，双指针former和latter间相距k步）。
  3. 双指针共同移动： 循环中，双指针former和latter每轮都向前走一步，直至former走过链表尾节点时跳出（跳出后，latter与尾节点距离为k−1，即latter指向倒数第k个节点）。
  4. 返回值： 返回latter即可。

时间复杂度分析

链表总共遍历两次，所以时间复杂度是$O(n)$。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    ListNode* getKthFromEnd(ListNode* head, int k) {
		int n = 0;
        for(auto p = head; p; p = p->next) n++;
        if(k > n) return nullptr;
        auto p = head;
        for(int i = 0; i < n - k; ++i) p = p->next;
        return p;
    }
};
/* 双指针*/
class Solution {
public:
    ListNode* getKthFromEnd(ListNode* head, int k) {
        ListNode* former = head;
        ListNode* latter = head;
        for(int i = 0; i < k; i++)
            former = former->next;
        while(former != nullptr) {
            former = former->next;
            latter = latter->next;
        }
        return latter;
    }
};

链表中环的入口结点

给定一个链表，若其中包含环，则输出环的入口节点。若其中不包含环，则输出null。

样例

1
2
3
给定如上所示的链表：[1, 2, 3, 4, 5, 6]
输入：2（2表示编号是2的节点，节点编号从0开始。所以编号是2的节点就是val等于3的节点）
输出：环的入口节点3.

思路

链表，快慢指针扫描——Floyd算法，$O(n)$

  1. 走a+nb步一定是在环入口
  2. 第一次相遇时慢指针已经走了nb步

这类链表题目一般都是使用双指针法解决的，例如寻找距离尾部第K个节点、寻找环入口、寻找公共尾部入口等。

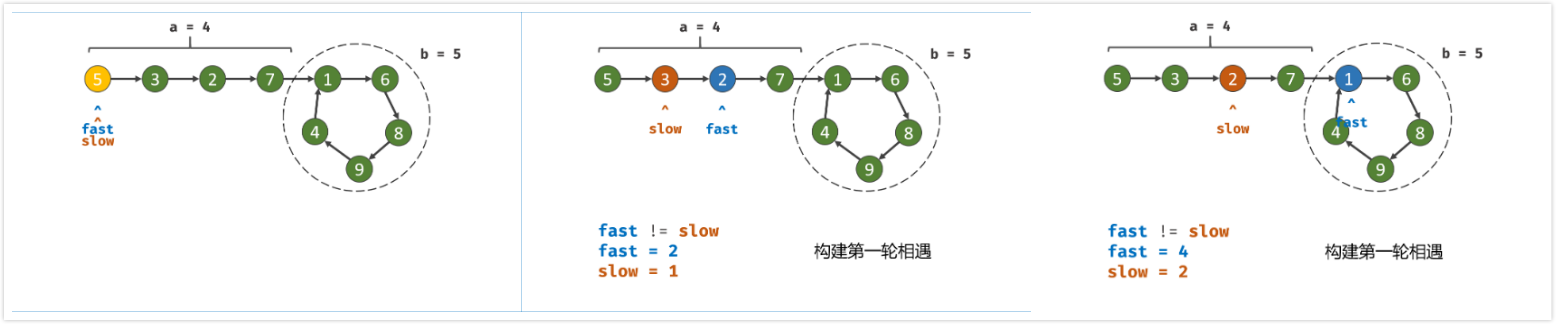
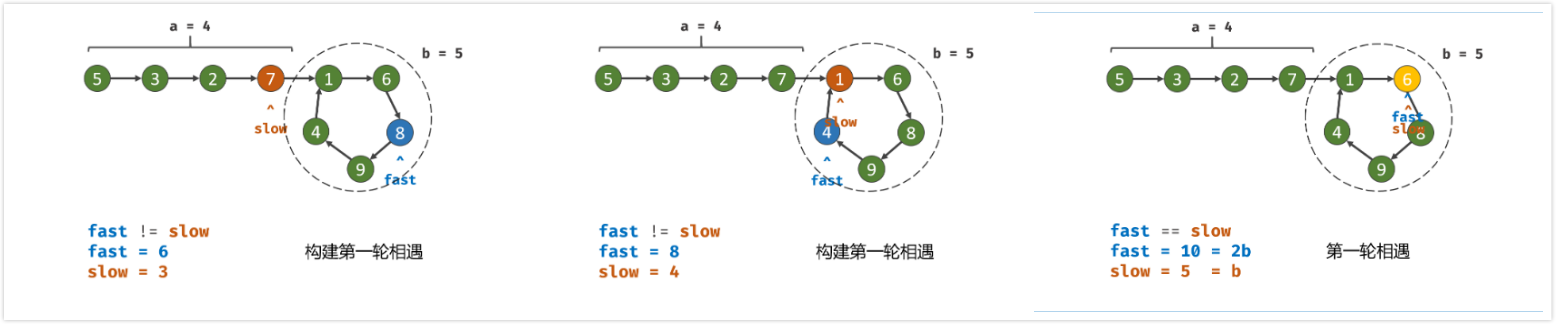
  1. 双指针第一次相遇： 设两指针 fast，slow 指向链表头部 head，fast 每轮走2步，slow 每轮走1步；

    1. 第一种结果： fast 指针走过链表末端，说明链表无环，直接返回 null；（TIPS：若有环，两指针一定会相遇。因为每走1轮，fast 与 slow 的间距+1，fast 终会追上 slow； ）

    2. 第二种结果： 当fast == slow时， 两指针在环中 第一次相遇 。下面分析此时fast 与 slow走过的 步数关系 ：

      • 设链表共有a+b个节点，其中链表头部到链表入口有a个节点（不计链表入口节点），链表环有b个节点（这里需要注意，a和b是未知数，例如图解上链表a=4,b=5）；设两指针分别走了f，s步，则有：

        1. fast 走的步数是slow步数的2倍，即f=2s；（解析： fast 每轮走2步）
        2. fast比slow多走了n个环的长度，即f=s+nb；（ 解析： 双指针都走过a步，然后在环内绕圈直到重合，重合时fast比slow多走环的长度整数倍 ）；

      • 以上两式相减得：f=2nb，s=nb，即fast和slow指针分别走了2n，n 环的周长 （注意： n是未知数，不同链表的情况不同）。

  2. 目前情况分析：

    1. 如果让指针从链表头部一直向前走并统计步数k，那么所有走到链表入口节点时的步数是：k=a+nb。
    2. 而目前，slow指针走过的步数为nb步。因此，我们只要想办法让 slow再走a步停下来，就可以到环的入口。
    3. 但是我们不知道a的值，该怎么办？依然是使用双指针法。我们构建一个指针，此指针需要有以下性质：此指针和slow一起向前走a步后，两者在入口节点重合。那么从哪里走到入口节点需要a步？答案是链表头部head。

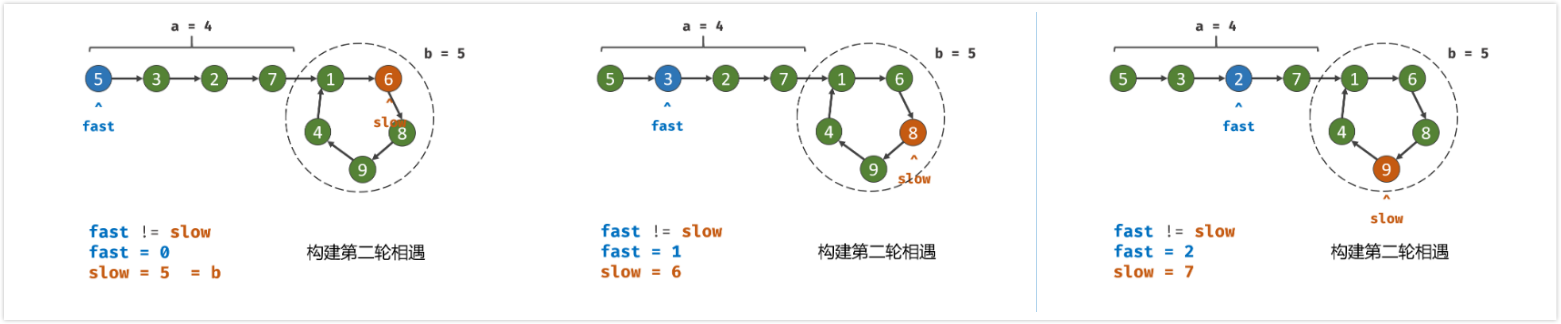
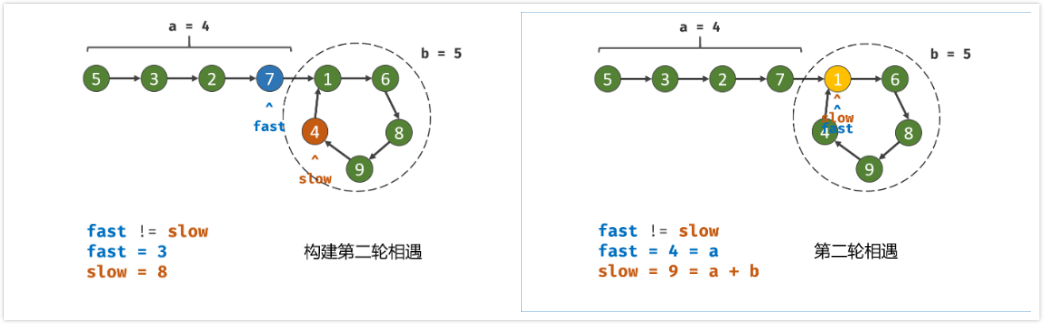
  3. 双指针第二次相遇：

    1. slow指针 位置不变 ，将fast指针重新指向链表头部节点 ；slow和fast同时每轮向前走1步； （ TIPS：此时f=0，s=nb； ）
    2. 当 fast 指针走到f=a步时，slow 指针走到步s = a+nb，此时 两指针重合，并同时指向链表环入口 。

  4. 返回slow指针指向的节点。

时间复杂度分析

第二次相遇中，慢指针须走步数a<a+b；第一次相遇中，慢指针须走步数a+b−x<a+b，其中x为双指针重合点与环入口距离；因此总体为线性复杂度$O(n)$

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if (!head || !head->next) return 0;				// 判断链表是否为空
        ListNode *fast = head, *slow = head;			// 初始化快慢指针
        while (fast && slow)
        {
            slow = slow->next;			// 慢指针走一步
            fast = fast->next;			// 快指针走两步
            if (fast) fast = fast->next; 			// 快指针是否走出链表结尾
            else return 0;
            if (fast == slow)			// 第一次快慢指针相遇
            {
                fast = head;				// 从头开始
                while (fast != slow)
                {
                    fast = fast->next;
                    slow = slow->next;
                }
                return slow;				// 第二次相遇则返回慢指针
            }
        }
        return 0;
    }
};
-------------本文结束 感谢您的阅读-------------

本文标题:剑指Offer——Week2

文章作者:善雯

发布时间:2020年07月11日 - 14:07

最后更新:2020年07月15日 - 20:07

原始链接:http://shanwenyang.github.io/2020/07/11/Offer-Week2/

许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。

原创技术分享，您的支持将鼓励我继续创作
0%