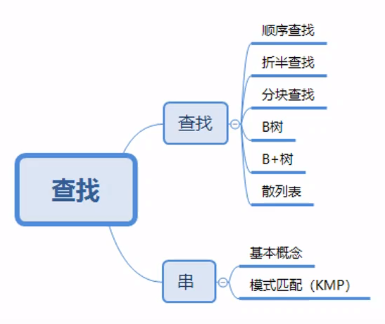
基本概念
定义:在数据结构中寻找满足某种条件的数据元素的过程,查找成功与查找失败。
查找表:用于查找的数据集合,由同一种数据类型(或记录)的组成,可以是一个数组或链表等数据类型。
操作:
- 查询某个特定的数据元素是否在查找表中
- 检索满足条件的某个特定的数据元素的各种属性
- 在查找表中插入一个元素
- 从查找表中删除一个元素
前两种:静态查找表;前四个:动态查找表
关键字:数据元素中唯一标识该元素的某个数据项的值,使用基于关键字的查找,查找结果应该是唯一的。
平均查找长度:查找时,关键字比较次数的平均值——$ASL=\sum_{i=1}^nP_iC_i$
顺序查找
最简单,最好理解。从头开始进行比较。
也称为线性查找(可以有序,也可以无序),主要用于在线性表中进行查找。
无序线性表的顺序查找
无序线性表进行顺序查找,查找失败时要遍历整个线性表
1 | typedef struct{ |
平均查找长度:
$ASL_{success}=\sum_{i=1}^n P_iC_i=\sum_{i=1}^nP_i(n-i+1)=\sum_{i=1}^n\frac{1}{n}*(n-i+1)=\frac{n+1}{2}$
$ASL_{failed}=\sum_{i=1}^nP_iC_i=\sum_{i=1}^n\frac{1}{n}*(n+1)=n+1$
有序线性表的顺序查找
对关键字有序线性表进行顺序查找,查找失败不一定要遍历整个线性表,遍历到比它大的元素就可以
判定树:描述查找过程的二叉排序树

平均查找长度:$n+1$个失败节点
$ASL_{failed}=\sum_{i=1}^nP_iC_i=\sum_{i=1}^n\frac{1}{n+1}=\frac{1+2+…+n+n}{n+1}=\frac{n}{2}+\frac{n}{n+1}$
折半查找(二分查找)
仅适用于有序表的顺序表——数组
思想:
- 首先将给定值key与表中中间位置的元素进行比较
- 若相等,就返回该元素的位置
- 若不等,则在前半部分或后半部分进行查找
查找升序序列时:
- 若key小于中间元素,则查找前半部分
- 若key大于中间元素,则查找后半部分
重复该过程,直到查找到元素为止;或者查找失败
1 | int Binary_Search(SeqList L, ElemType key){ |
判定树:
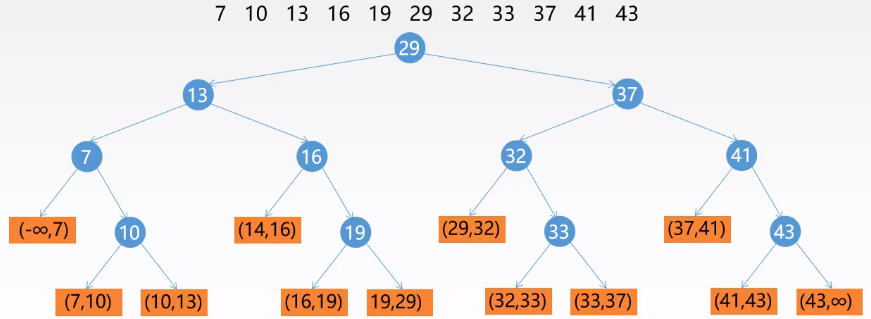
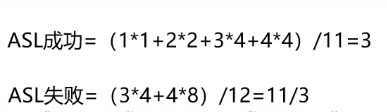
平均查找效率:成功——$log_2(n+1)$
顺序查找适用于顺序存储和链式存储,序列有序无序皆可;折半查找只适用于顺序存储,且要求序列一定有序
分块查找
索引序列查找,吸取了顺序查找和折半查找的各自优点,既有动态结构,又适用于快速查找。
分块:块内无序块间有序
- 将查找表分成若干子块,块内的元素可以无序,但是快间有序的,即对于所有块有第
i块的最大关键字小于第i+1块的所有记录的关键字。 - 建立索引表,索引表中每个元素含有各块的最大关键字和各块中第一个元素的地址,索引表按照关键字有序排列。
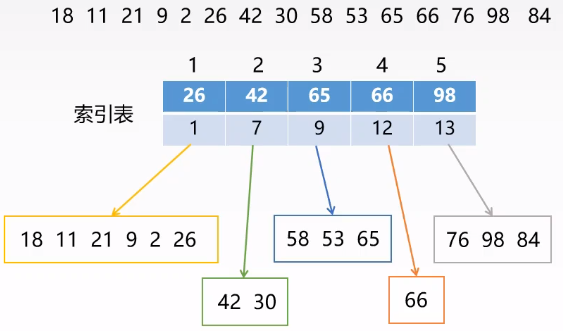
查找:两步
- 在索引表中确定待查记录所在的块,可以顺序查找也可以折半查找索引表。
- 在块内进行顺序查找。
平均查找长度:
分块查找的平均查找长度为索引查找($LI$)和块内查找($LS$)之和。
设长度为$n$的查找表均匀分为b块,每块记录有$s$个记录。
成功——$L_i+L_s$
若块内和块间均用顺序查找:成功——$L_i+L_s=\frac{s^2+2s+n}{2s}=\sqrt n +1$
若块内采用顺序查找,块间使用折半查找:成功——$L_i+L_s=log_2(b+1)+\frac{s+1}{2}$
B树
B树的阶:又称为多路平衡查找树,B树中所有结点的孩子结点数的最大值成为B树的阶。
特性:一棵$m$阶$B$树或为空树,或为满足以下条件的$m$叉树:
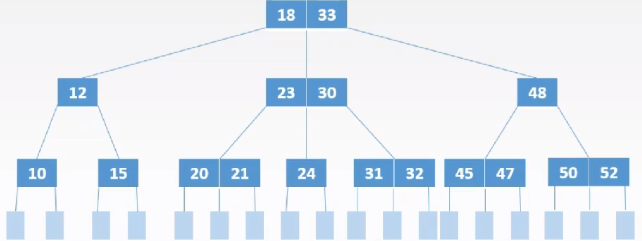
- 树中每个节点至多有$m$棵子树(即至多含有$m-1$个关键字)
- 若根节点不是终端节点,则至少有两棵子树
- 除根节点之外,所有的非叶子结点至少有$m/2$取上界棵子树(即$m/2$取上界$-1$个关键字)
- 非叶结点的结构:

$K_i$($i\in 1,2,…,n$)为结点的关键字,$K_1<K_2<…<K_n$,
$P_i(i=0,1,2,…,n)$为子树根节点的指针,$P_{i-1}$所指子树的关键字均小于$K_i$,$P_i$所指子树的关键字均大于$K_i$。
- 所有叶结点都出现在同一层上,并不带任何信息
$n$个关键字,阶数为$m$,高度为$h$的$B$树:
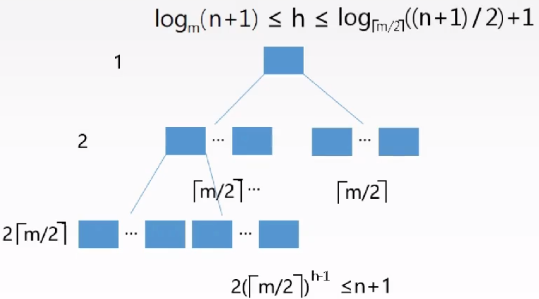
查找:
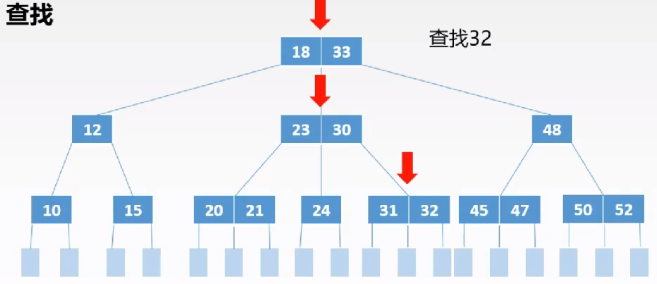
- 在$B$树中查找结点——磁盘
- 在结点中找关键字——内存
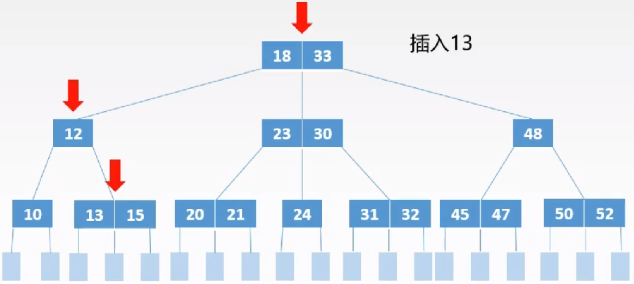
插入:
定位:查找插入该关键字的位置,即最底层某个非叶子结点(规定一定是插入在最底层的某个非叶子结点内,不需要调整)
插入:若插入后,不会破坏$m$阶二叉树的定义,即插入后结点关键字个数在属于区间[$m/2$上界$-1$,$m-1$],则直接插入;