反转链表
定义一个函数,输入一个链表的头结点,反转该链表并输出反转后链表的头结点。
思考题:
- 请同时实现迭代版本和递归版本。
样例
1 | 输入:1->2->3->4->5->NULL |
思路
链表操作,迭代,$O(n)$
翻转即将所有节点的next指针指向前驱节点。
由于是单链表,我们在迭代时不能直接找到前驱节点,所以我们需要一个额外的指针保存前驱节点。同时在改变当前节点的next指针前,不要忘记保存它的后继节点。
算法时间复杂度
只遍历一次链表,时间复杂度是 $O(n)$
C++代码
1 | class Solution { |
合并两个排序链表
输入两个递增排序的链表,合并这两个链表并使新链表中的结点仍然是按照递增排序的。
样例
1 | 输入:1->3->5 , 2->4->5 |
思路
二路归并,$O(n)$
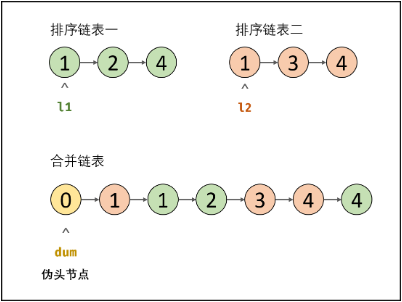
- 初始化: 伪头节点$dummy$ ,节点$cur$ 指向$dummy$。
- 循环合并: 当$l_1$或$l_2$为空时跳出;
- 当$l_1->val
val$时,$cur$的后继结点指向$l_1$,并且$l_1$向前走一步; - 当$l_1->val>=l_2->val$时,$cur$的后继结点指向$l_2$,并且$l_2$向前走一步;
- 结点$cur$向前走一步,即$cur=cur->next$。
- 当$l_1->val
- 合并剩余尾部:跳出时有两种情况,即$l_1$为空或$l_2$为空;
- 若$l_1\neq null$:将$l_1$添加至结点$cur$之后;
- 否则:将$l_2$添加至阶段$cur$之后。
- 返回值:合并链表在伪头节点$dummy$之后,因此返回$dummy->next$。
算法时间复杂度
$O(m+n)$:分别为两个链表的长度
C++代码
1 | class Solution { |
树的子结构
输入两棵二叉树A,B,判断B是不是A的子结构。我们规定空树不是任何树的子结构。
样例
1 | 树A: |
思路
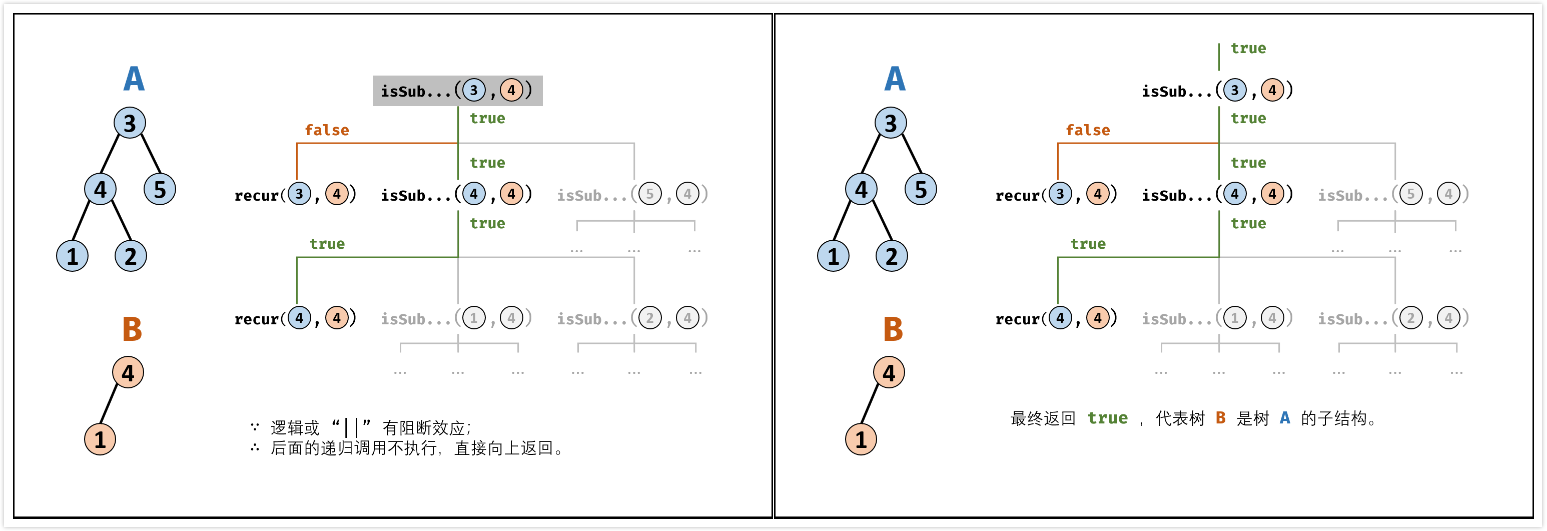
二叉树,递归,$O(nm)$
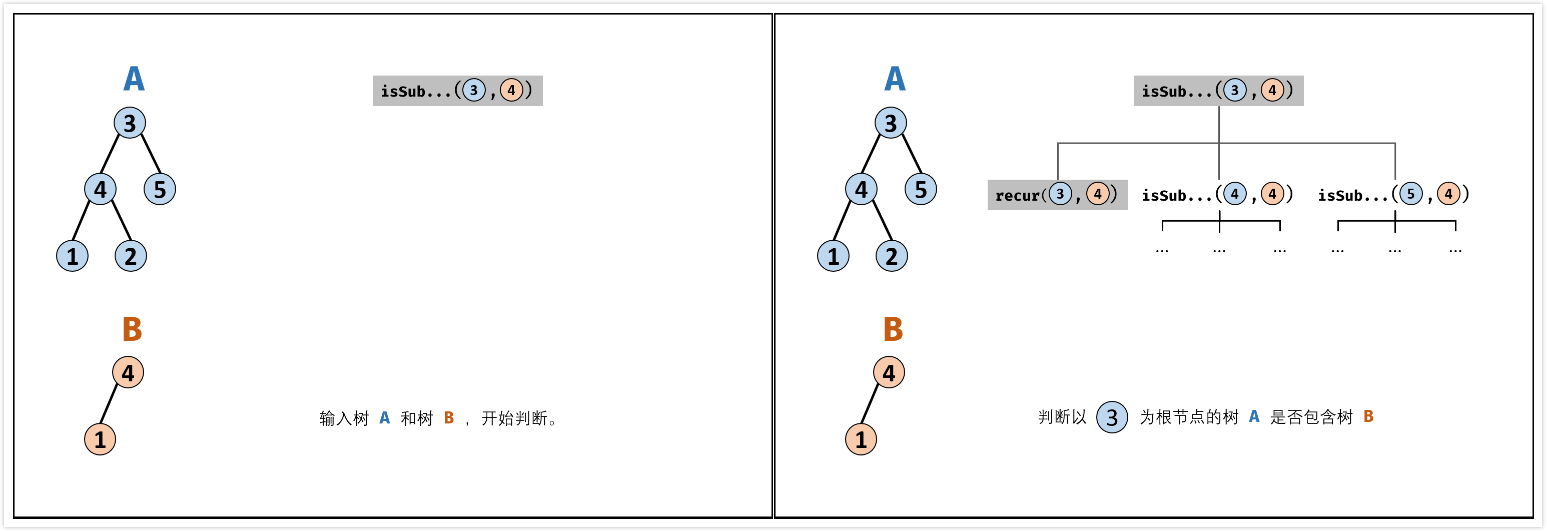
- 先序遍历树$A$中的每个结点$n_A$——对应函数:
isSubStructure(A, B) - 判断树$A$中以$n_A$为根节点的子树是否包含树$B$——对应函数:
recur(A, B)

步骤:
recur(A, B)函数:
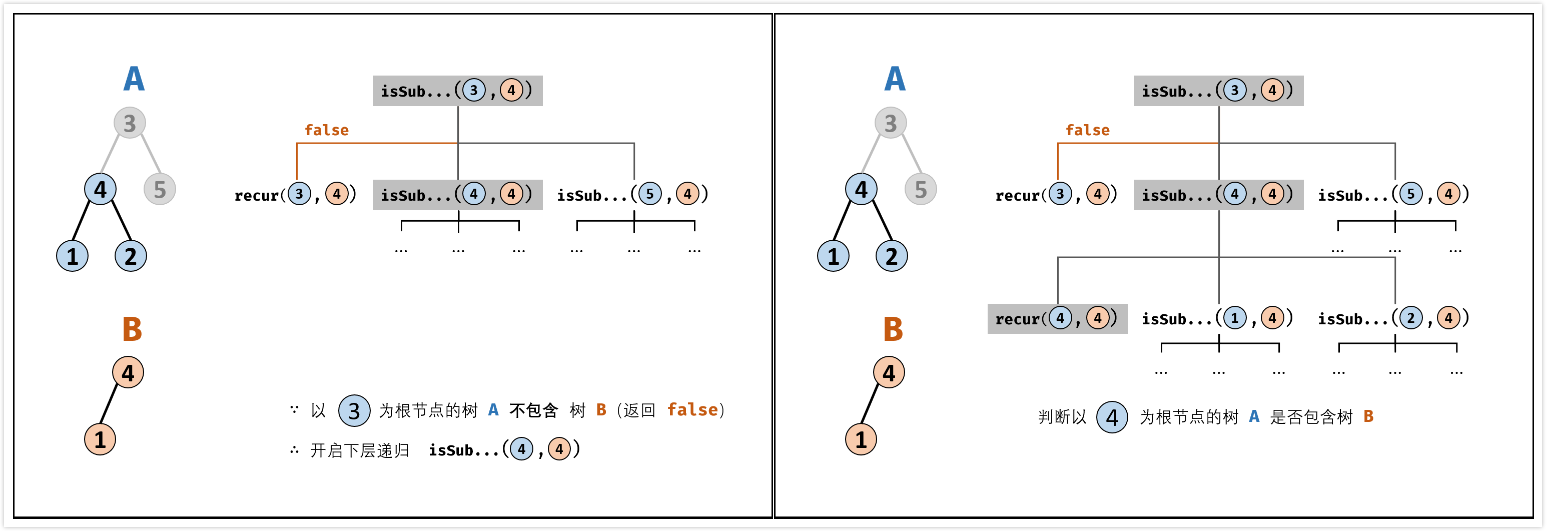
- 终止条件:
- 当节点$B$为空:说明树$B$已经匹配完成(越过叶子节点),因此返回
true; - 当节点$A$为空:说明已经越过树$A$的叶子节点,即匹配失败,返回
false; - 当节点$A$和$B$的值不同:说明匹配失败,返回
false;
- 当节点$B$为空:说明树$B$已经匹配完成(越过叶子节点),因此返回
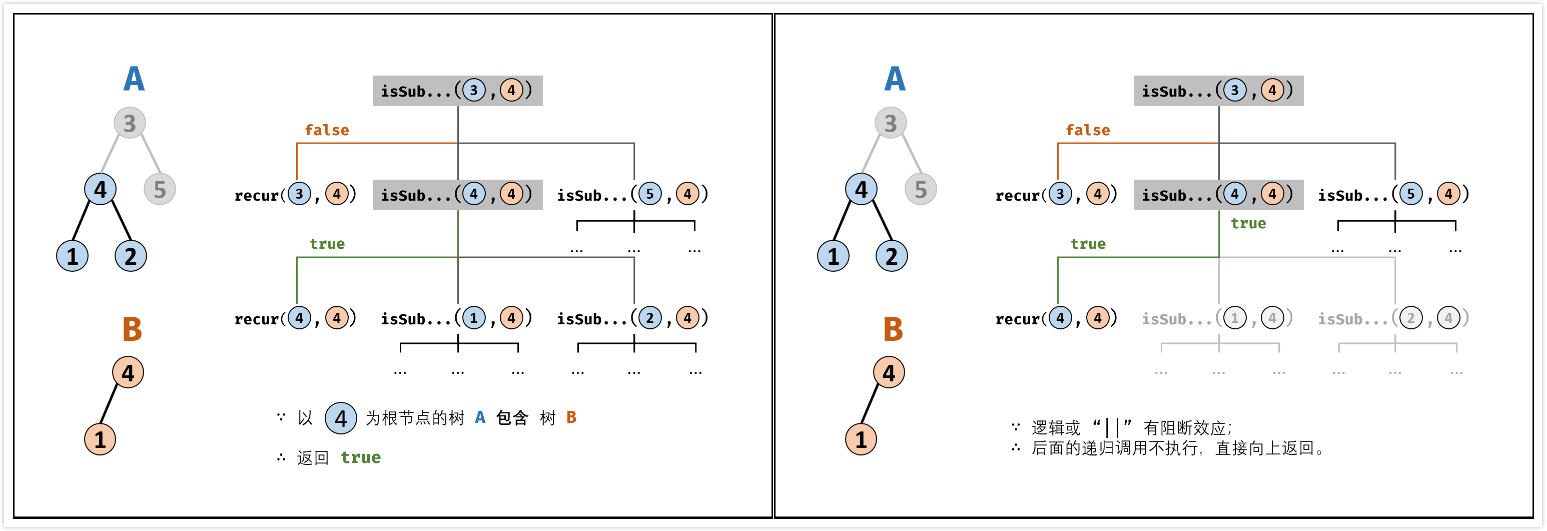
- 返回值:
- 判断$A$和$B$的左子节点是否相等,即
recur(A.left, B.left); - 判断$A$和$B$的右子节点是否相等,即
recur(A.right, B.right);
- 判断$A$和$B$的左子节点是否相等,即
isSunStructure(A, B)函数:
- 特例处理:当树$A$为空或者树$B$为空时,返回
false; - 返回值:若树$B$是树$A$的子结构,必须满足以下三种情况之一,用
||连接;- 以节点$A$为根节点的子树包含树$B$ ,对应
recur(A, B); - 树$B$是树$A$左子树的子结构,对应
isSubStructure(A.left, B); - 树$B$是树$A$右子树的子结构,对应
isSubStructure(A.right, B);
- 以节点$A$为根节点的子树包含树$B$ ,对应
算法时间复杂度分析
$O(nm)$:分别为两棵树的节点数量
C++代码
1 | class Solution { |
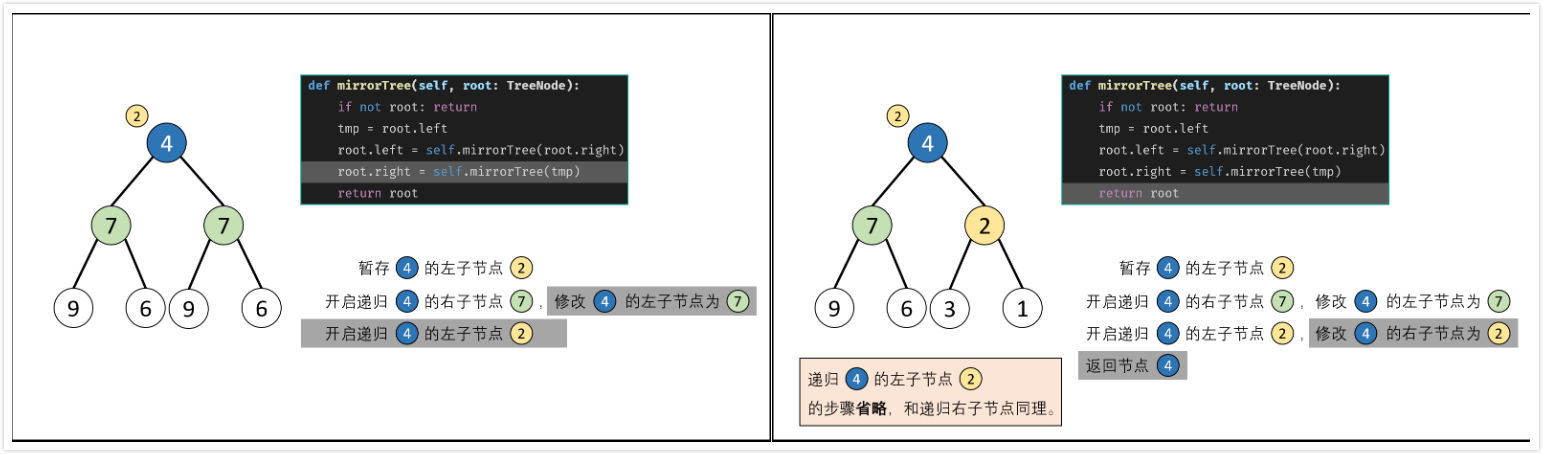
二叉树的镜像
输入一个二叉树,将它变换为它的镜像。
样例
1 | 输入树: |
思路
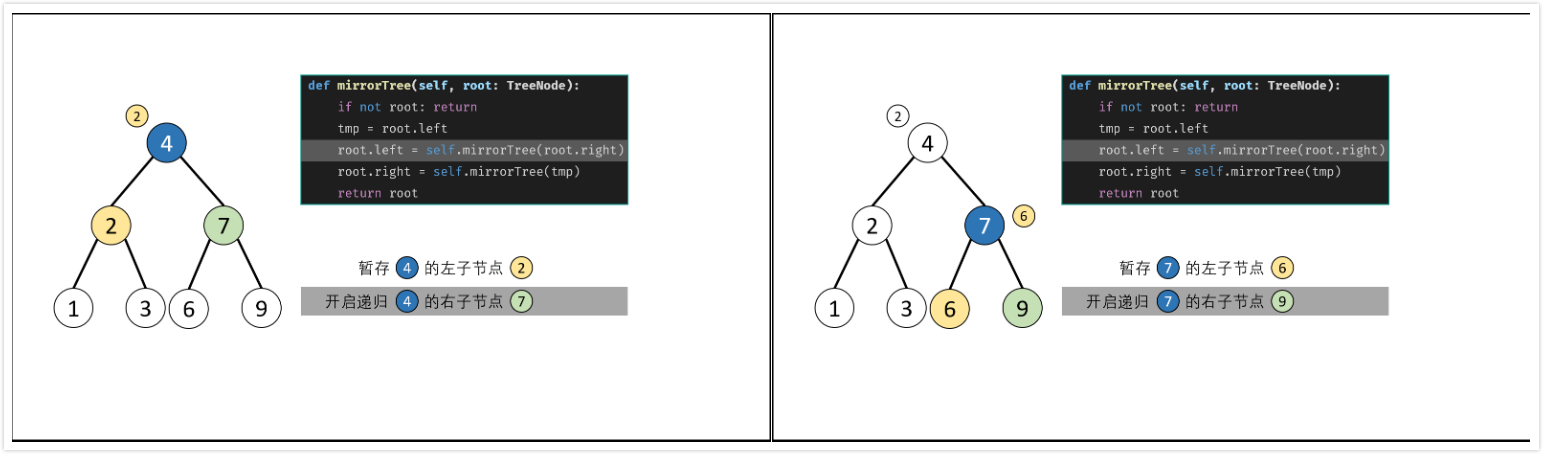
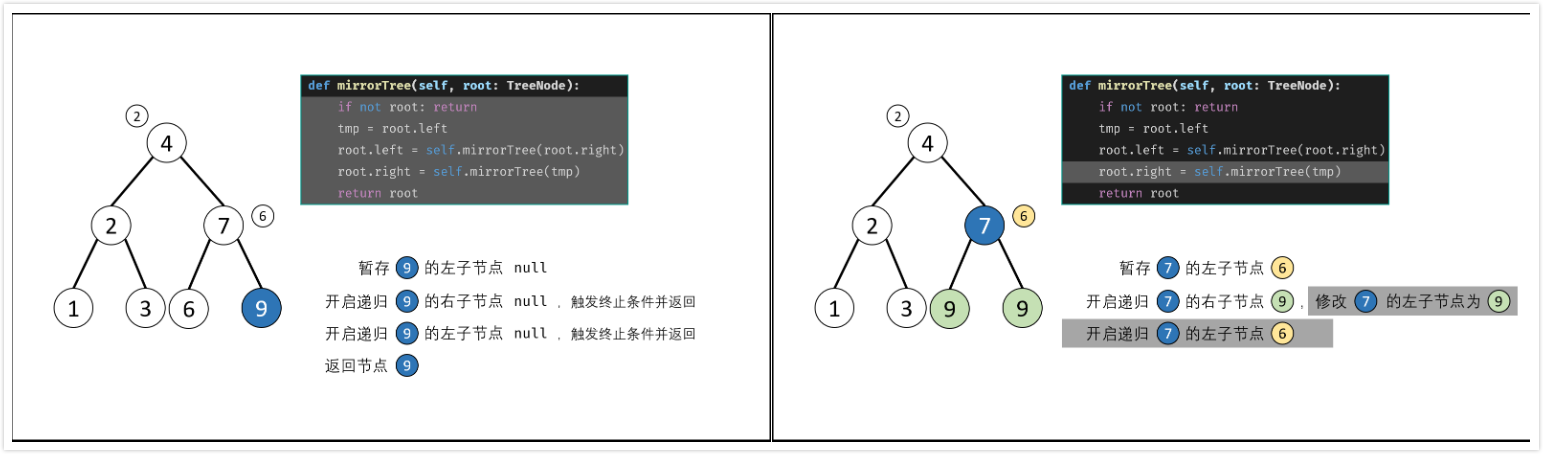
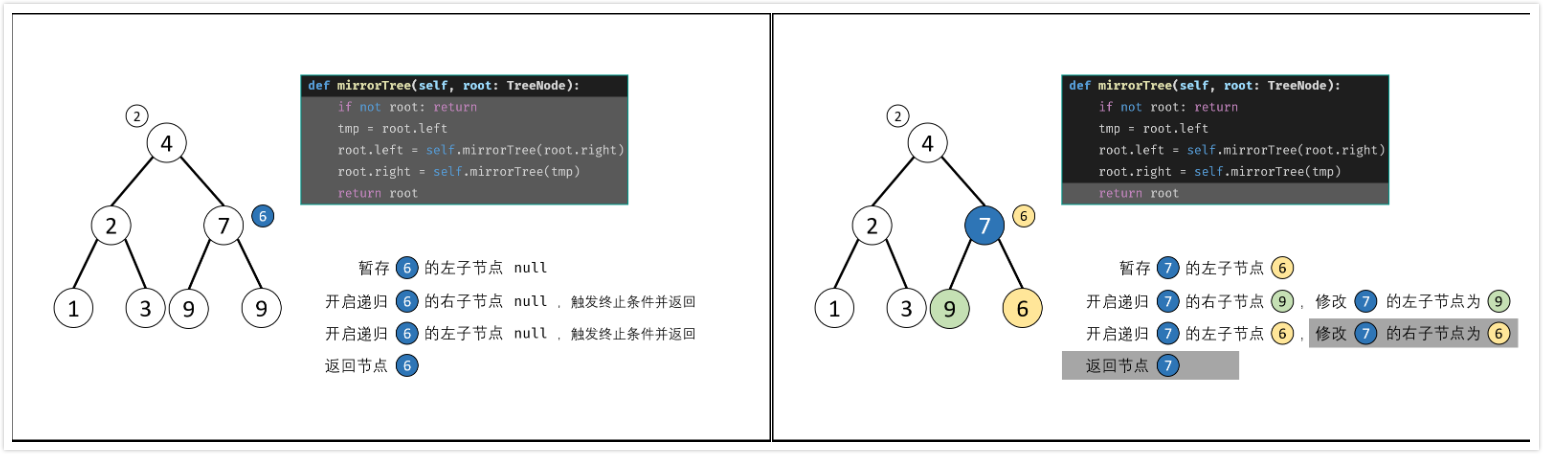
递归,$O(n)$
- 根据二叉树镜像的定义,递归二叉树交换每个节点的左/右子节点。
- 终止条件:当节点$root$为空时(即越过叶子节点),返回
nullptr; - 递归条件:
- 初始化节点$tmp$,用于暂存$root$的左子节点;
- 开启递归右子节点
mirrorTree(root->right),并返回值作为$root$的左子节点; - 开启递归左子节点
mirrorTree(tmp),并返回值作为$root$的右子节点;
- 返回值:返回房前节点$root$。
Q: 为何需要暂存$root$的左子节点?
A: 在递归右子节点root->left = mirrorTree(root->right);执行完毕后,root->left的值已经发生改变,此时递归左子节点mirrorTree(root->left)则会出问题。
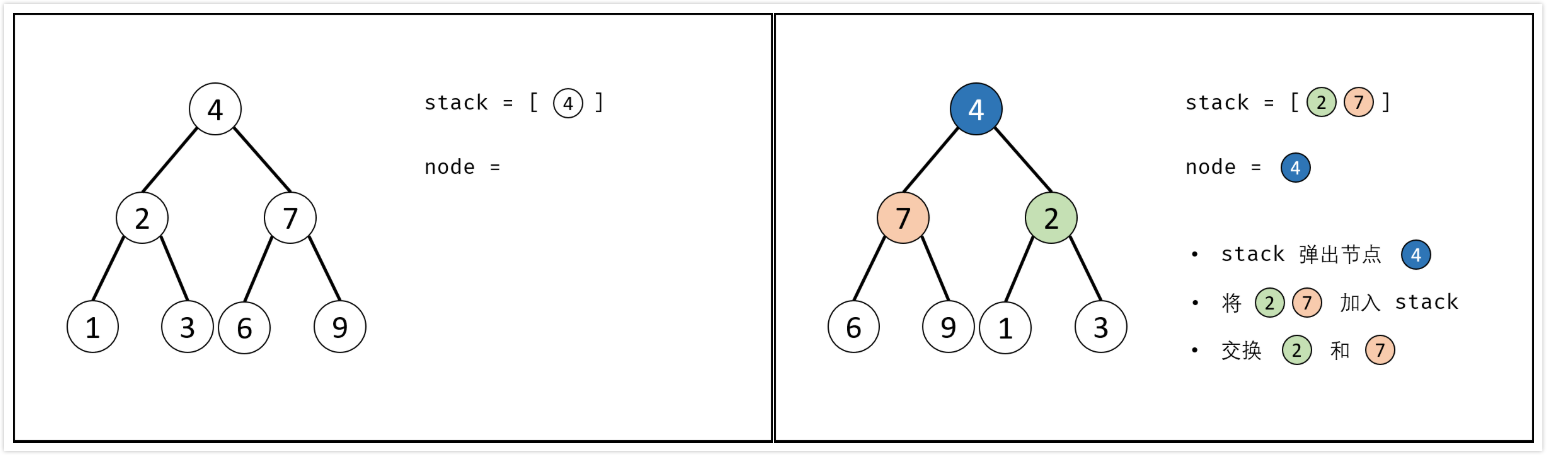
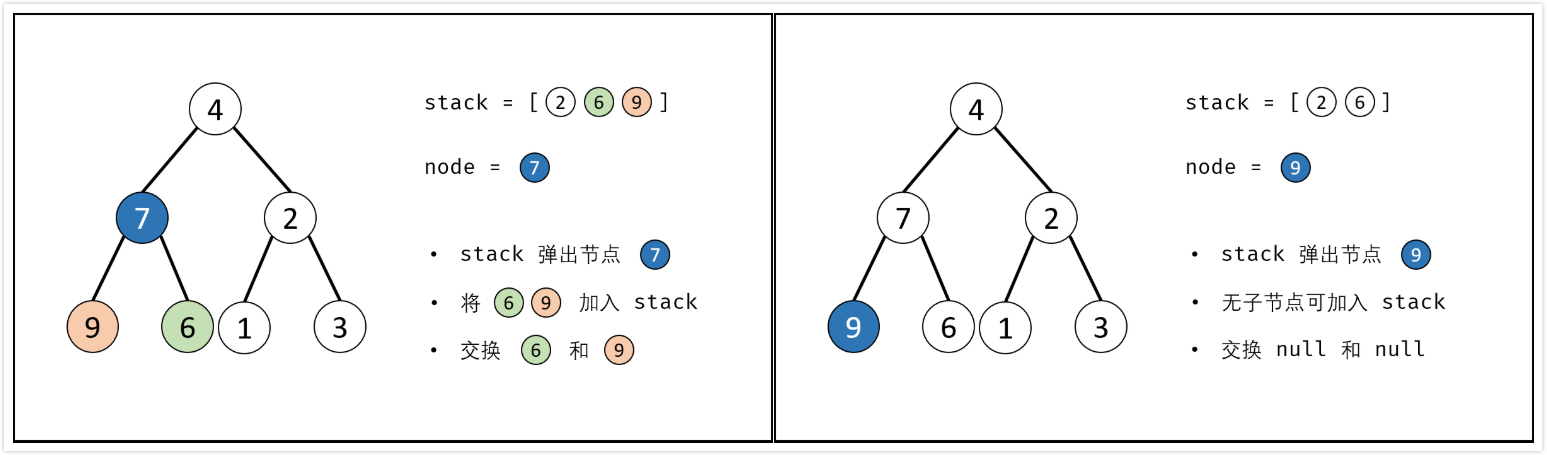
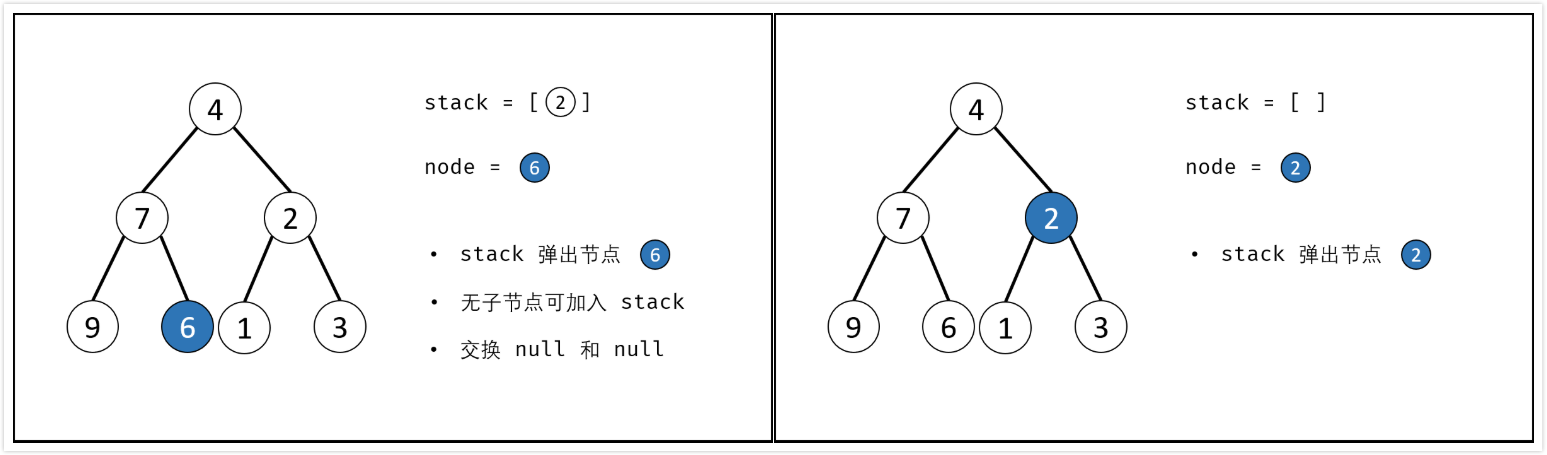
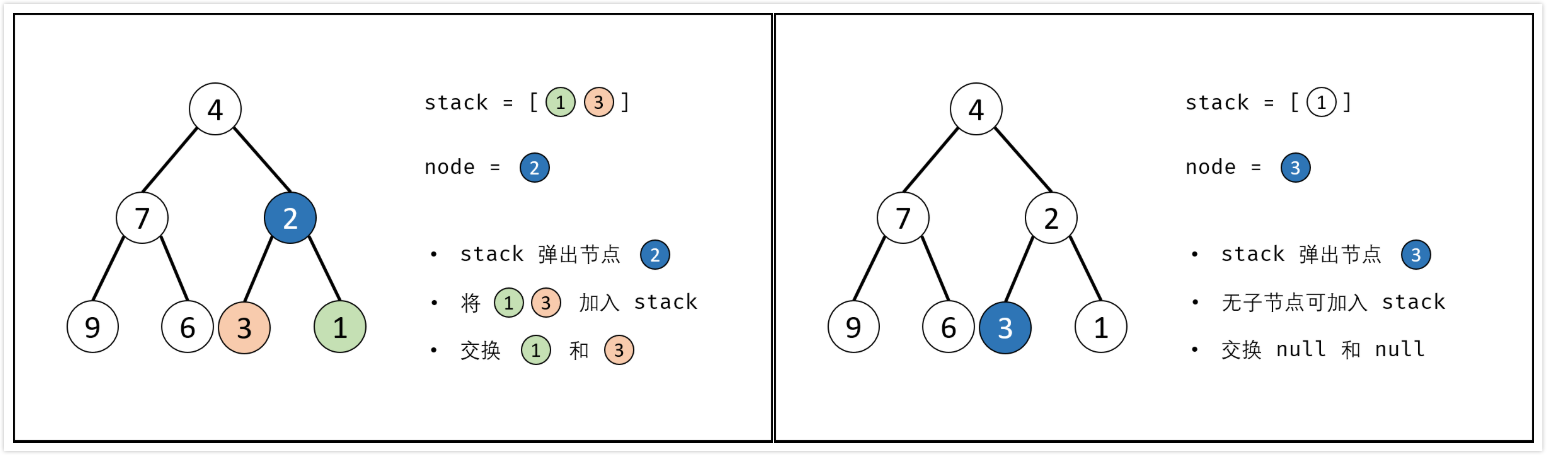
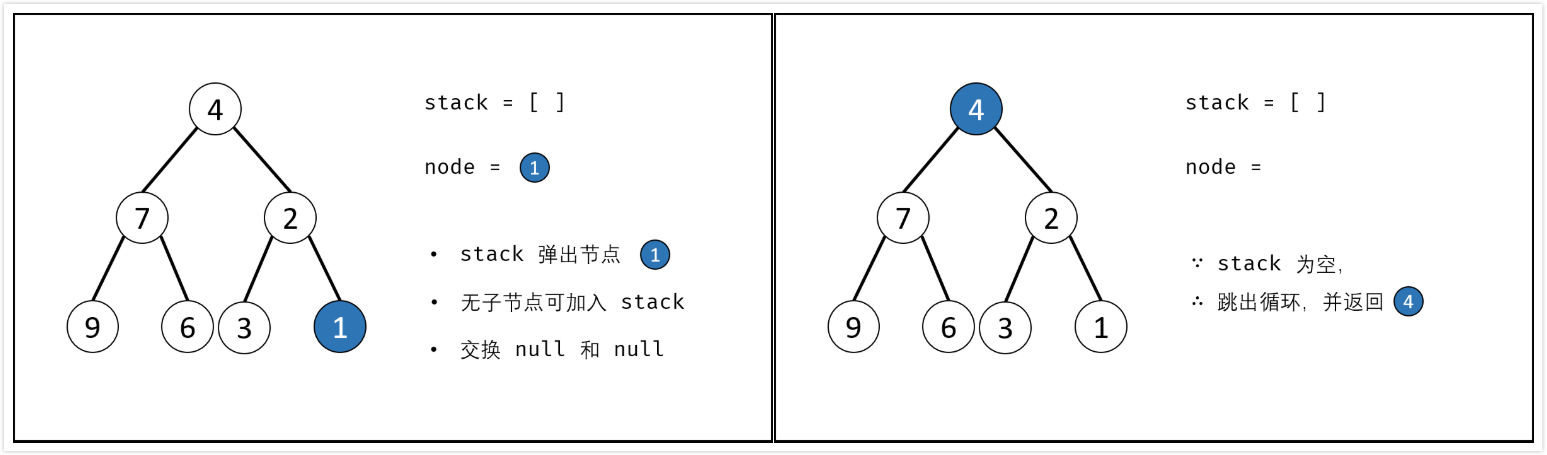
辅助栈:
- 利用栈(或队列)遍历树的所有节点$node$,并交换每个$node$的左/右子节点
- 特例处理:当节点$root$为空时,返回
nullptr; - 初始化:栈(或队列),并加入根节点$root$;
- 循环交换:当栈$stack$为空时跳出;
- 出栈:记为$node$;
- 添加子节点:将$node$左和右子节点入栈;
- 交换:交换$node$的左/右子节点。
- 返回值:返回根节点$root$
算法时间复杂度
时间复杂度$O(N)$ : 其中$N$为二叉树的节点数量,建立二叉树镜像需要遍历树的所有节点,占用$O(N)$时间。
C++代码
1 | /* 递归 */ |
对称的二叉树
请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。
样例
1 | 如下图所示二叉树[1,2,2,3,4,4,3,null,null,null,null,null,null,null,null]为对称二叉树: |
思路
自上而下递归,二叉树,$O(n)$
isSynmetric(root):
- 特例处理:若根节点$root$为空,直接返回
true; - 返回值:即
recur(root->left, root->right);
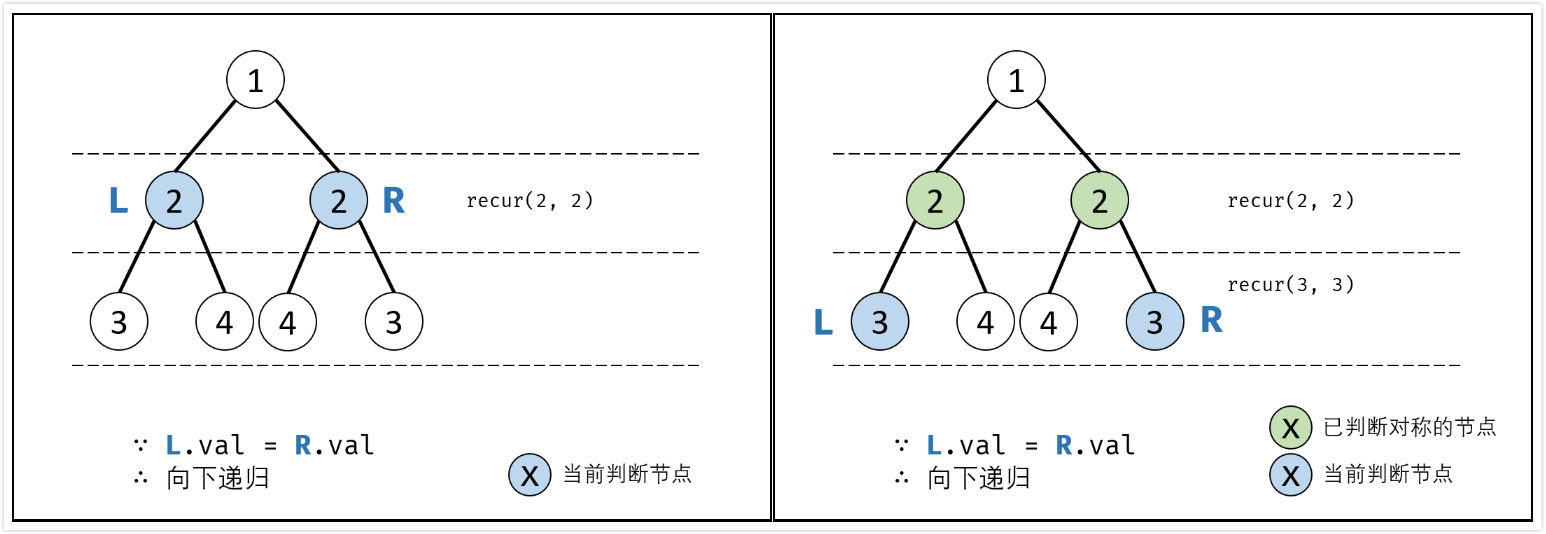
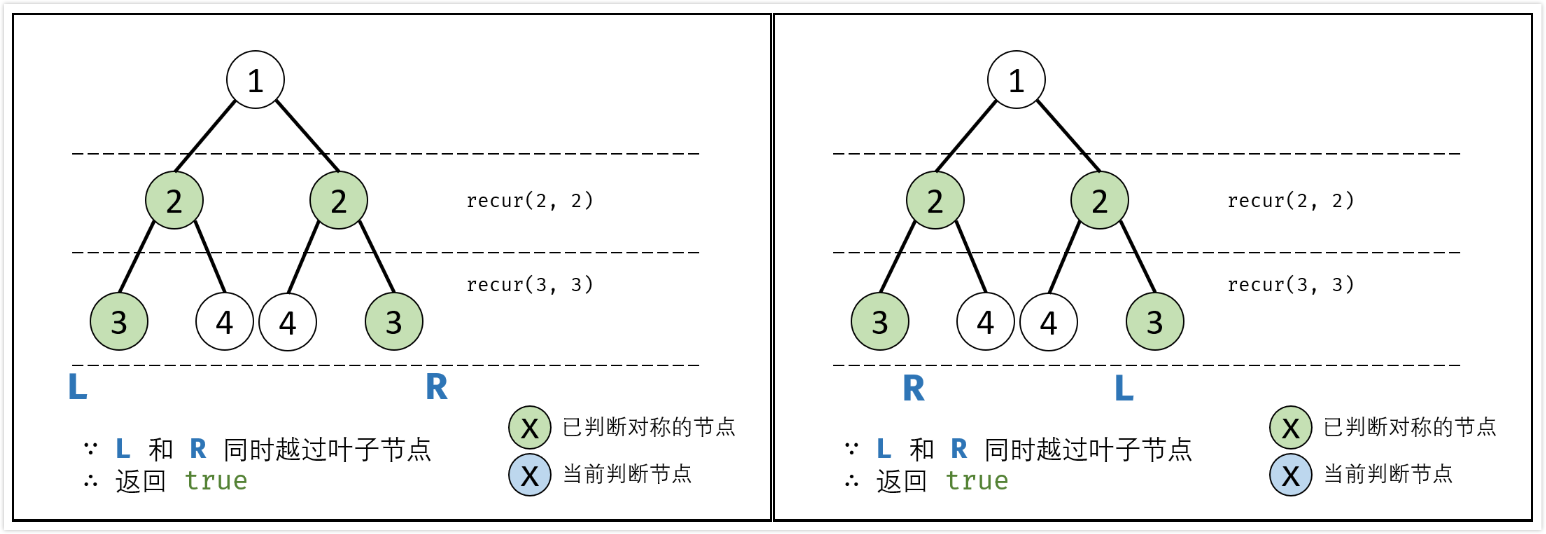
recur(L, R):
- 终止条件:
- 当$L$和$R$同时越过叶子节点:此树自上而下的节点都对称,返回
true; - 当$L$或$R$中只有一个越过叶节点:此树步对称,因此返回
false; - 当节点$L->val \neq R->val$:此树不对称,因此返回
false;
- 当$L$和$R$同时越过叶子节点:此树自上而下的节点都对称,返回
- 递推工作:
- 判断两个节点$L->left$和$R->right$是否对称:
recur(L->left, R->right); - 判断两个节点$L->right$和$R->left$是否对称:
recur(L->right, R->left);
- 判断两个节点$L->left$和$R->right$是否对称:
- 返回值:两对节点对称时,才是对称树,逻辑与
&&。
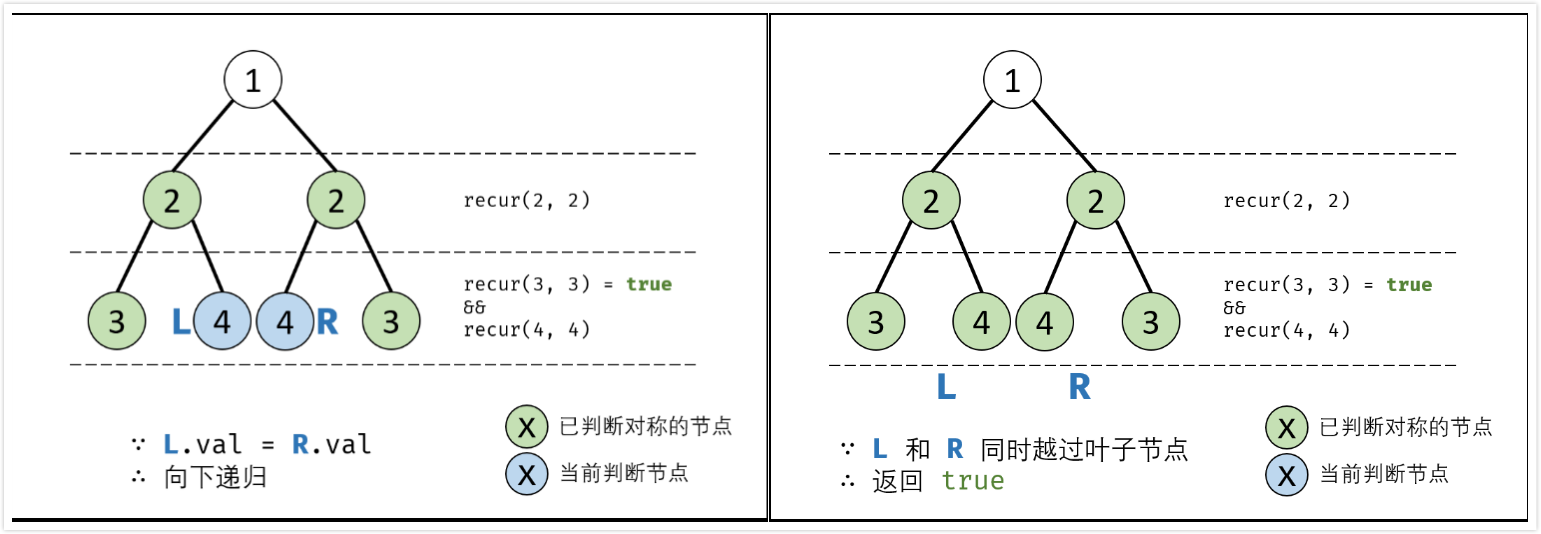
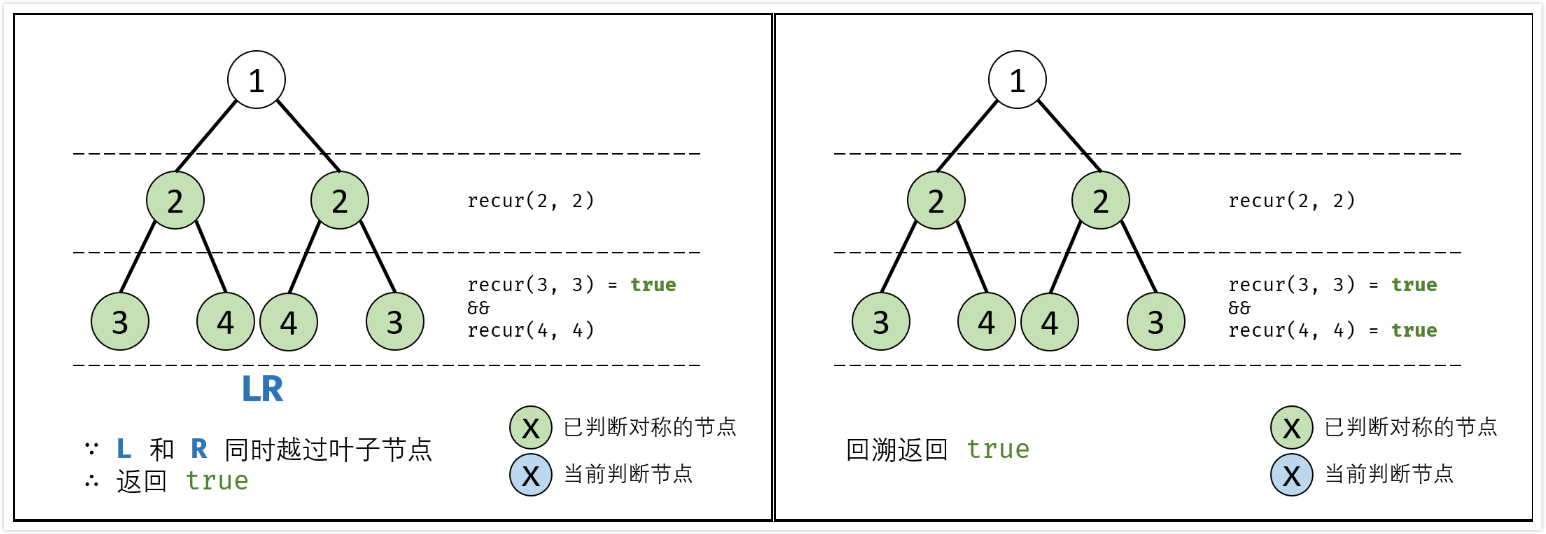
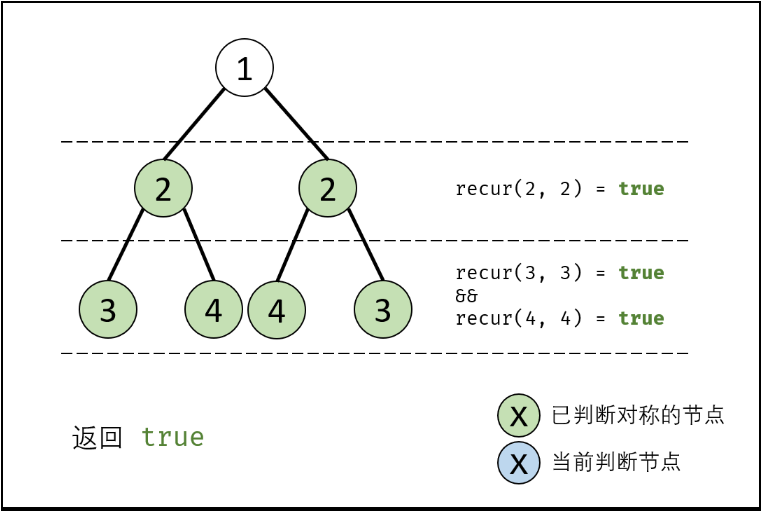
算法时间复杂度
$O(n)$:其中$n$为二叉树的节点数量
C++代码
1 | class Solution { |
顺时针打印矩阵
输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字。
样例
1 | 输入: |
思路
模拟,$O(n^2)$
- 顺时针定义四个方向:上、右、下、左。
- 从左上角开始遍历,先往右走,走到不能走为止;
- 然后更改到下个方向,再走到不能走为止;
- 依次类推,遍历$n^2$ 个格子后停止。
算法时间复杂度
矩阵中每个格子遍历一次,所以总时间复杂度是$O(n^2)$。
C++代码
1 | class Solution { |
包含min函数的栈
设计一个支持push,pop,top等操作并且可以在O(1)时间内检索出最小元素的堆栈。
- push(x)–将元素x插入栈中
- pop()–移除栈顶元素
- top()–得到栈顶元素
- min()–得到栈中最小元素
样例
1 | MinStack minStack = new MinStack(); |
思路
辅助栈(单调栈)
函数设计:
push(x)函数:保持栈$B$的元素是严格降序的;- 将$x$压入栈$A$(即
push(x)); - 若栈$B$为空
|| x <= B.top(),则将$x$压入栈$B$(即B.push(x))。
- 将$x$压入栈$A$(即
pop()函数:保持栈$A$、$B$的元素一致性;- 执行
A.pop(),将出战元素记为y; - 若
y == B.top(),则执行$B$出栈(即B.pop())。
- 执行
top()函数:直接返回栈$A$的栈顶元素即可(A.top());min()函数:直接返回栈$B$的栈顶元素即可(B.top());
算法时间复杂度
push(), pop(), top(), min() 四个函数的时间复杂度均为常数级别$O(1)$。
C++代码
1 | class MinStack { |
栈的压入、弹出序列
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。
注意:若两个序列长度不等则视为并不是一个栈的压入、弹出序列。若两个序列都为空,则视为是一个栈的压入、弹出序列。
样例
1 | 输入:[1,2,3,4,5] |
思路
模拟,辅助栈,$O(n)$
- 入栈: 按照压栈序列的顺序执行。
- 出栈: 每次入栈后,循环判断“栈顶元素 == 弹出序列的当前元素”是否成立,将符合弹出序列顺序的栈顶元素全部弹出。
流程:
- 初始化:辅助栈
stack,弹出序列的索引i; - 遍历压栈序列:各元素记为
num;- 元素
num入栈; - 循环出栈:若
stack.top() == popped[i]; ++i;;
- 元素
- 返回值:若
stack为空,则此弹出序列合法
算法时间复杂度
时间复杂度$O(N)$: 其中$N$为列表$pushed$的长度;每个元素最多入栈与出栈一次,即最多共$2N$次出入栈操作。
C++代码
1 | class Solution { |
不分行从上往下打印二叉树(层次)
从上往下打印出二叉树的每个结点,同一层的结点按照从左到右的顺序打印。
样例
1 | 输入:[8, 12, 2, null, null, 6, null, 4, null, null, null] |
思路
BFS,层次遍历,$O(n)$
BFS 通常借助队列的先入先出特性来实现。
- 特例处理:当树的结点为空,直接返回
[] - 初始化:打印结果列表
res = [],包含根节点的队列queue = [root] - BFS循环:当队列
queue为空时跳出- 出队:队首元素出队,记为
node - 打印:将
node->val添加到列表res尾部 - 添加子节点:若
node的左(右)子树节点不空,则将左(右)子节点加入队列queue
- 出队:队首元素出队,记为
- 返回值:返回打印结果列表
res即可
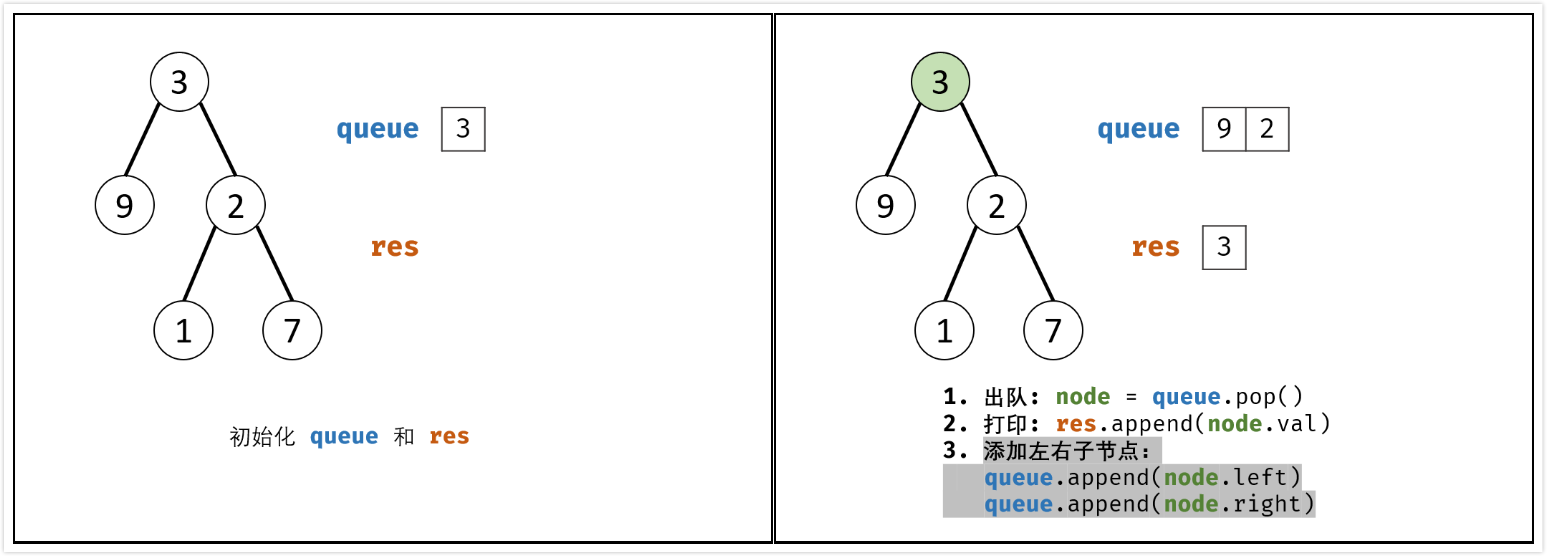
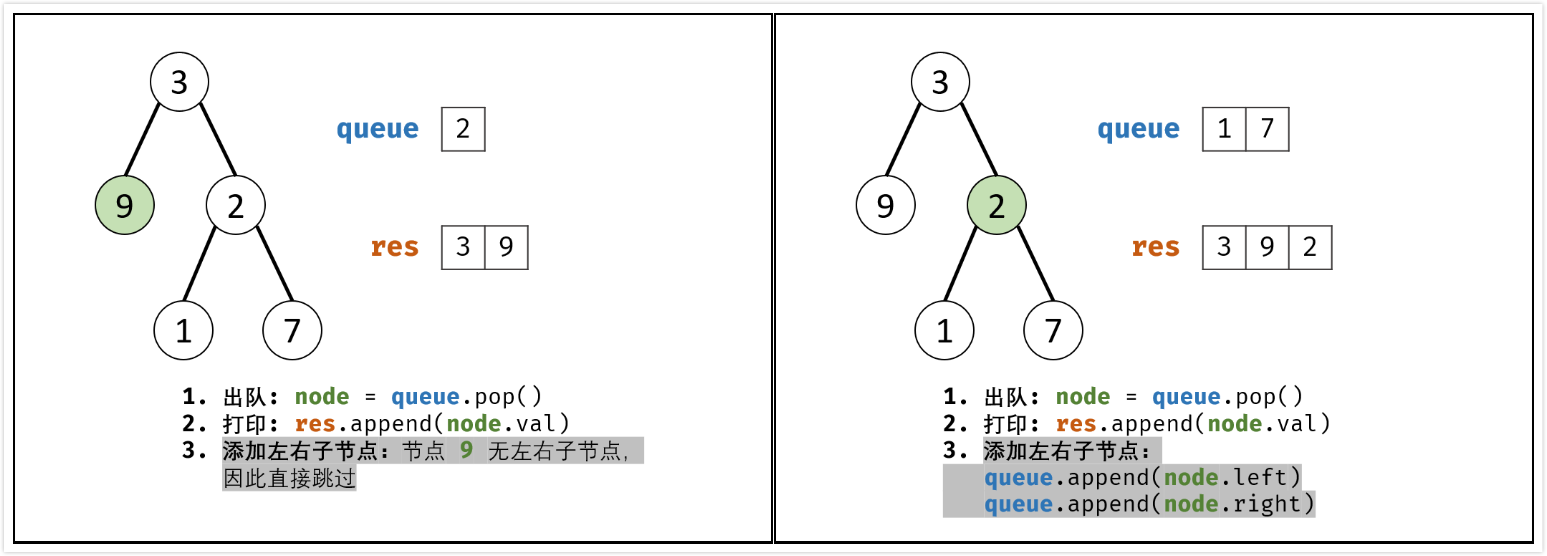
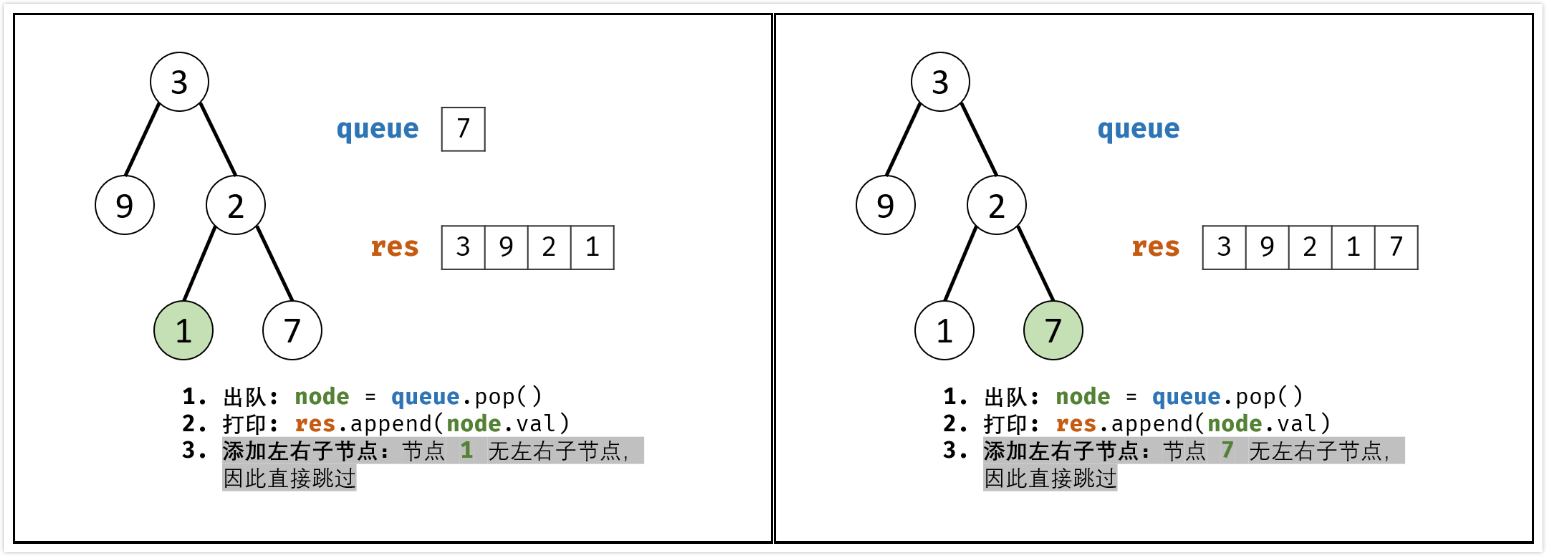
算法时间复杂度
时间复杂度$O(N)$:$N$为二叉树的节点数量,即BFS需循环$ N$次。
C++代码
1 | class Solution { |
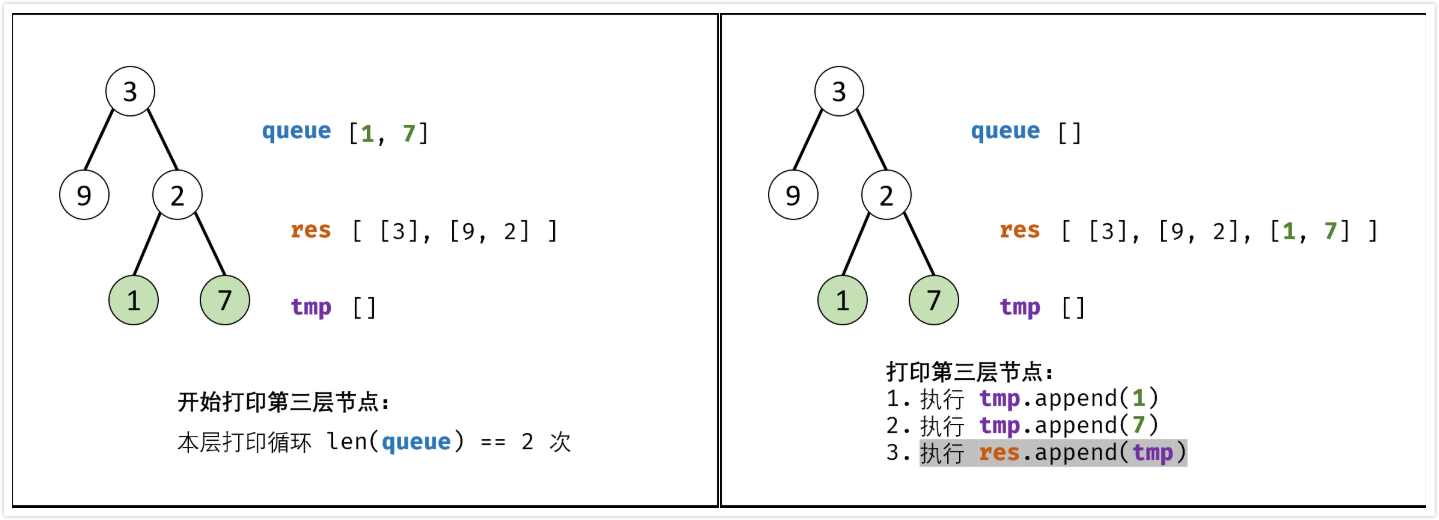
分行从上往下打印二叉树
从上到下按层打印二叉树,同一层的结点按从左到右的顺序打印,每一层打印到一行。
样例
1 | 输入:[8, 12, 2, null, null, 6, null, 4, null, null, null] |
思路
BFS,$O(n)$
- 特例处理:当树的结点为空,直接返回
[](同上) - 初始化:打印结果列表
res = [],包含根节点的队列queue = [root](同上) - BFS循环:当队列
queue为空时跳出- 新建一个临时列表
tmp,用于存储当前层的打印结果\ - 当前层打印循环:循环次数为当前层节点数(队列
queue长度)- 出队:队首元素出队,记为
node - 打印:将
node->val添加到列表tmp尾部 - 添加子节点:若
node的左(右)子树节点不空,则将左(右)子节点加入队列queue
- 出队:队首元素出队,记为
- 当前层结果
tmp添加到res
- 新建一个临时列表
- 返回值:返回打印结果列表
res即可
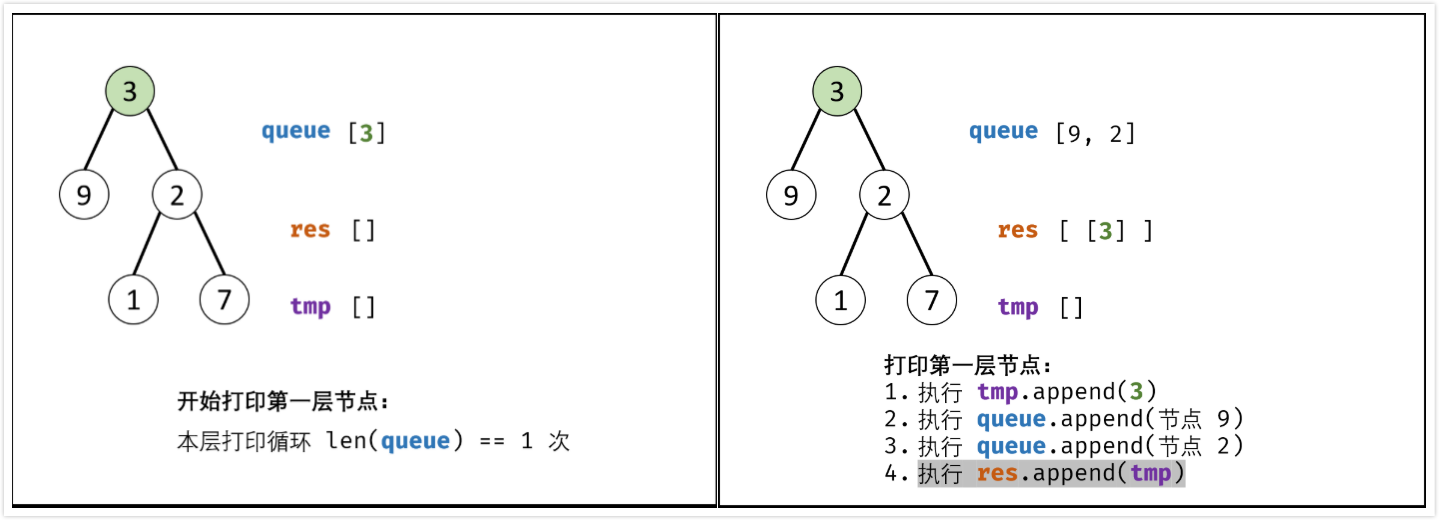
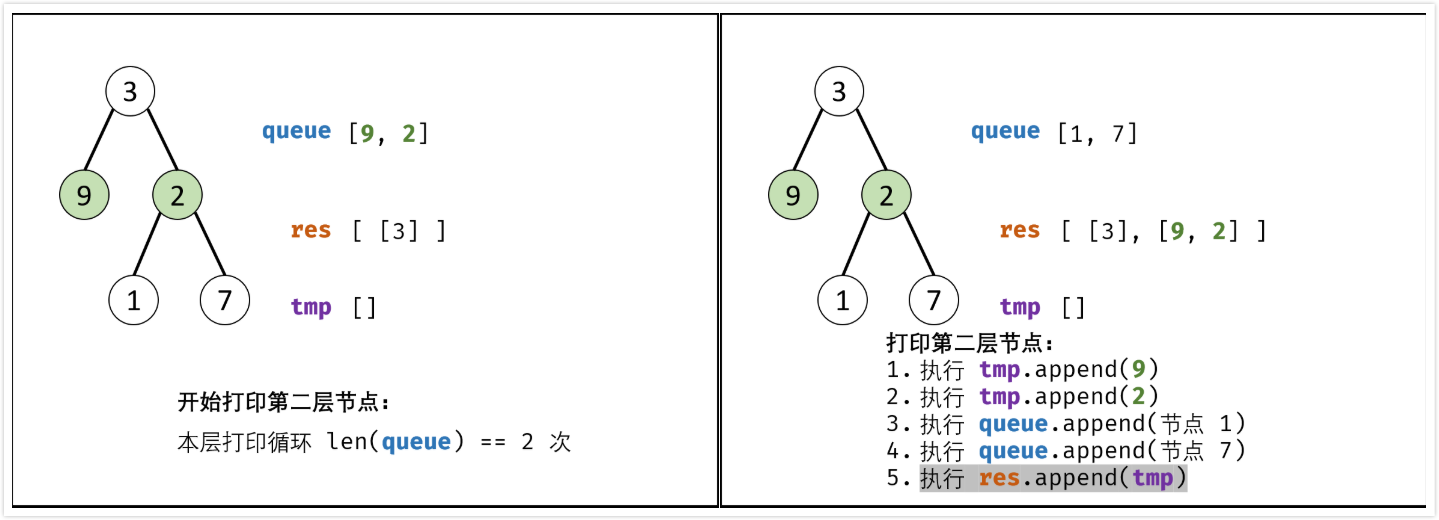
算法时间复杂度
时间复杂度$O(N)$:$N$为二叉树的节点数量,即BFS需循环$ N$次。
C++代码
1 | class Solution { |
Z字形打印二叉树
请实现一个函数按照之字形顺序从上向下打印二叉树。即第一行按照从左到右的顺序打印,第二层按照从右到左的顺序打印,第三行再按照从左到右的顺序打印,其他行以此类推。
样例
1 | 输入:[8, 12, 2, null, null, 6, 4, null, null, null, null] |
思路
BFS,$O(n)$
同上一题,偶数层倒叙(res.size() % 2 == 1),奇数层顺序(res.size() % 2 == 0)。
算法时间复杂度
时间复杂度$O(N)$:$N$为二叉树的节点数量,即BFS需循环$ N$次。
C++代码
1 | class Solution { |

