二叉搜索树的后序遍历

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则返回true，否则返回false。假设输入的数组的任意两个数字都互不相同。

样例

1 2	输入：[4, 8, 6, 12, 16, 14, 10] 输出：true

思路

递归，分治，$O(n^2)$

终止条件：当$l>=r$时，说明此子树节点数量$<=1$，无需判断正确性，直接返回true；
递归：
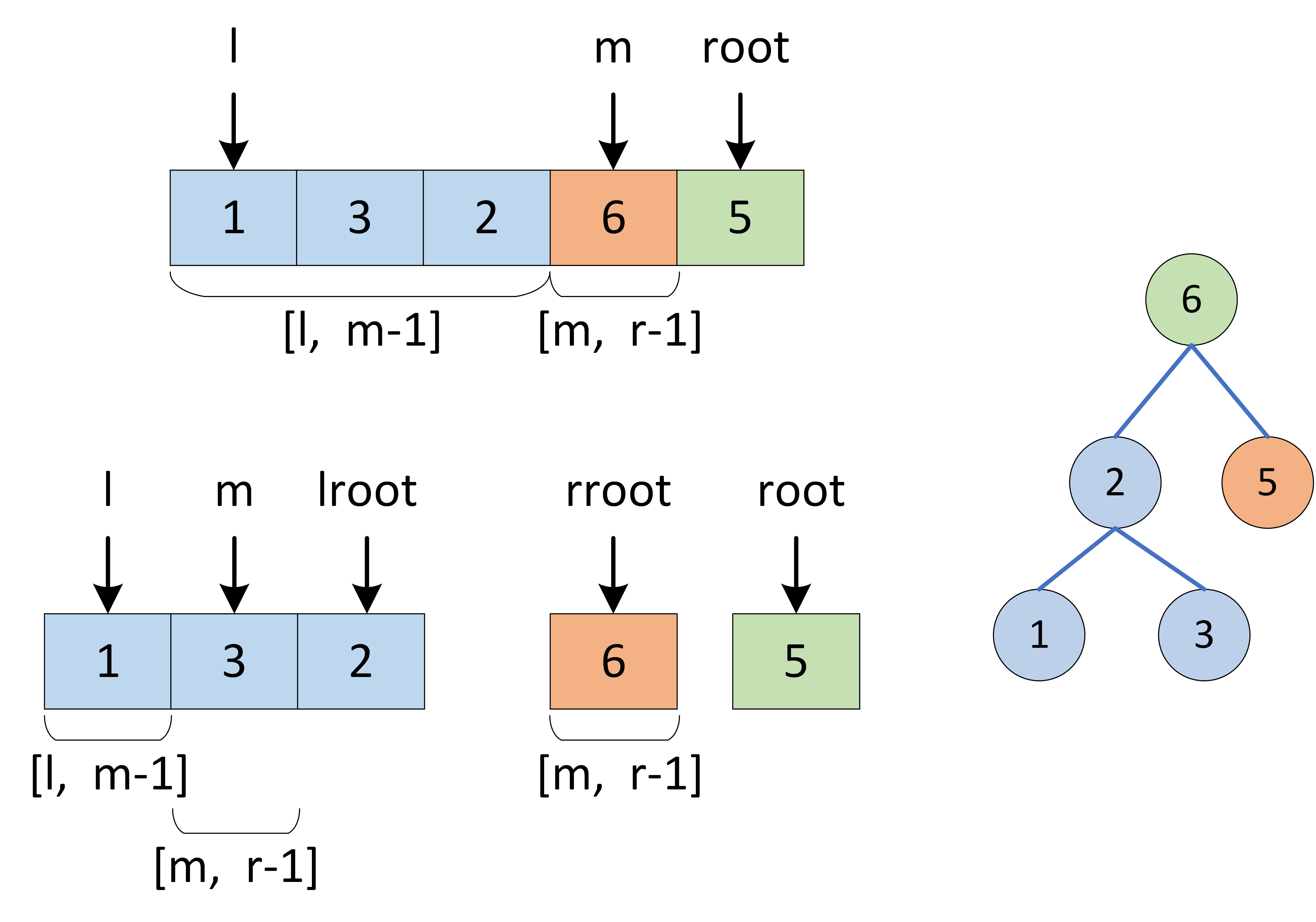
1. 划分左右子树：遍历后序序列的$[l,r]$区间元素，寻找第一个大于根节点的节点，索引记为$m$。此时，可划分出左子树区间$[l,m-1]$，右子树区间$[m,r-1]$，根节点索引为$r$。
2. 判断是否是二叉搜索树：
  1. 左子树区间$[l,m-1]$内所有节点都应该$<postorder[j]$。而第$1.$步已经保证左子树区间正确性，只需要判断右子树区间即可。
  2. 右子树区间$[m,j-1]$内所有节点都应该$>postorder[j]$。实现方式为遍历，当遇到$<postorder[j]$的节点则跳出，通过判断$p=j$判断是否为二叉搜索树。
返回值： 所有子树都需正确才可判定正确，因此使用与逻辑符&&连接。
1. p=j：判断此树是否正确。
2. recur(i, m - 1)：判断此树的左子树是否正确。
3. recur(m, j - 1)：判断此树的右子树是否正确。

时间复杂度$O(N^2)$)：每次调用recur(l,r)减去一个根节点，因此递归占用$O(N)$；最差情况下（即当树退化为链表），每轮递归都需遍历树所有节点，占用$O(N)$。

C++代码

class Solution {
public:
    bool verifyPostorder(vector<int>& postorder) {
        return recur(postorder, 0, postorder.size() - 1);
    }
    bool recur(vector<int>& postorder, int l, int r){
        if(l >= r) return true;
        int p = l;
        while(postorder[p] < postorder[r]) p++;
        int m = p;
        while(postorder[p] > postorder[r]) p++;
        return p == r && recur(postorder, l, m - 1) && recur(postorder, m, r - 1);
    }
};

二叉树中和为某一值的路径

输入一棵二叉树和一个整数，打印出二叉树中结点值的和为输入整数的所有路径。从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。

样例

给出二叉树如下所示，并给出num=22。
      5
     / \
    4   6
   /   / \
  12  13  6
 /  \    / \
9    1  5   1
输出：[[5,4,12,1],[5,6,6,5]]

思路

回溯法，$O(n)$

先序遍历，路径记录

pathSum(root, sum)函数：

初始化：结果列表res，路径path。
返回值：返回res即可。

recur(root,tar)函数：

递归参数：当前节点root，当前目标值tar。
终止条件：若节点root为空，则返回。
递归工作：
1. 路径更新：当前节点值root->val加入path
2. 目标值更新：tar=tar-root->val（即目标值tar从sum减到0）
3. 路径记录：当root为叶子且路径和等于目标值，将此路径path加入到res
4. 先序遍历：递归左右子节点
5. 路径恢复：向上回溯，需要将当前节点从路径path中删除，执行path.pop()

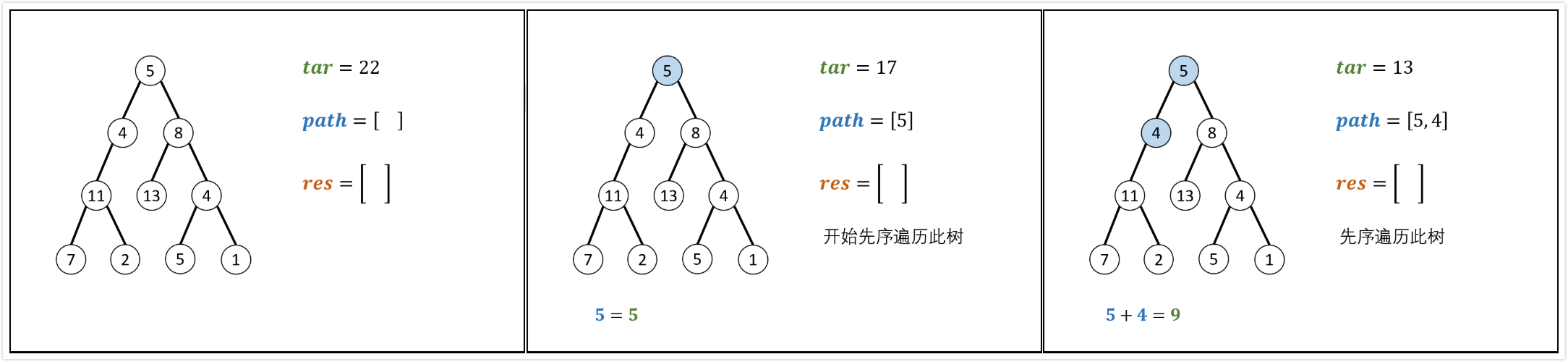
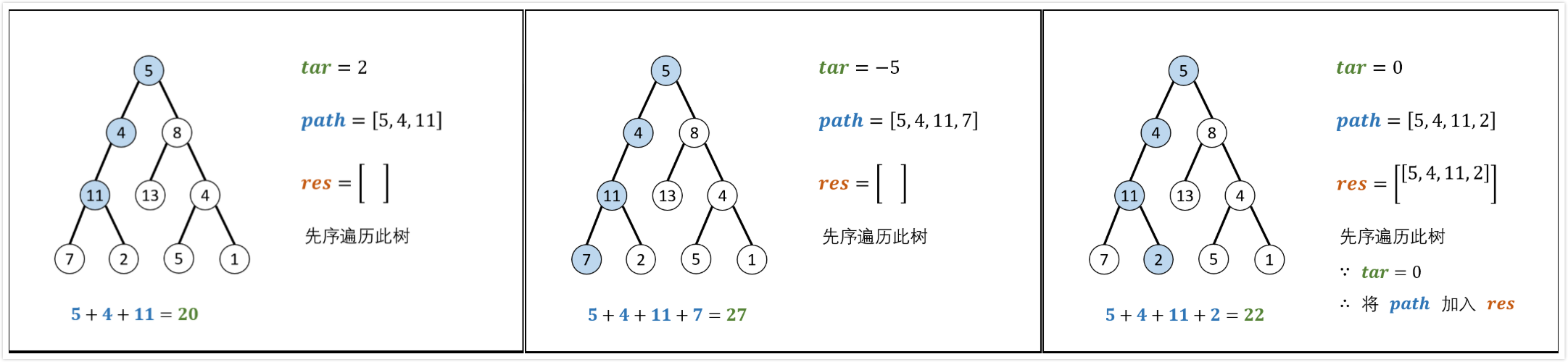
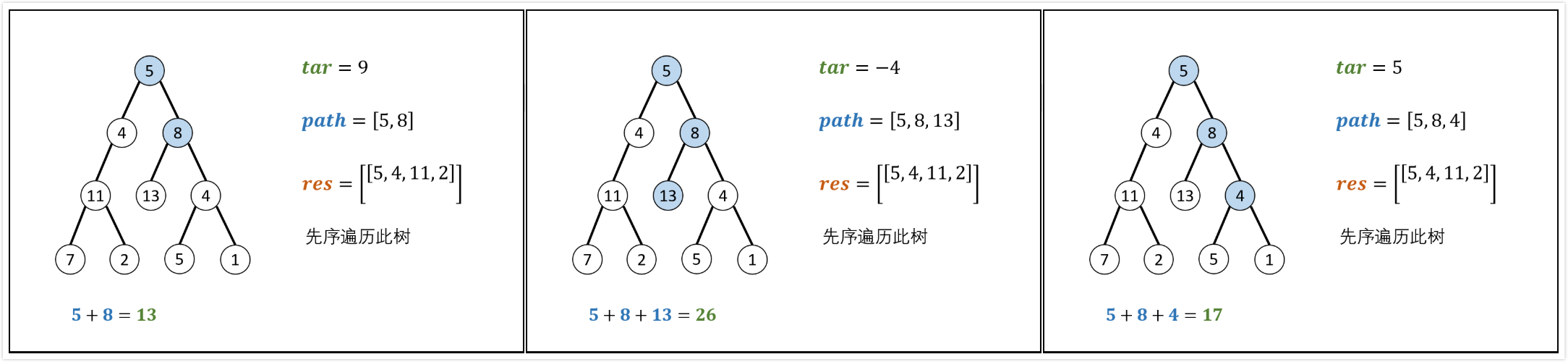
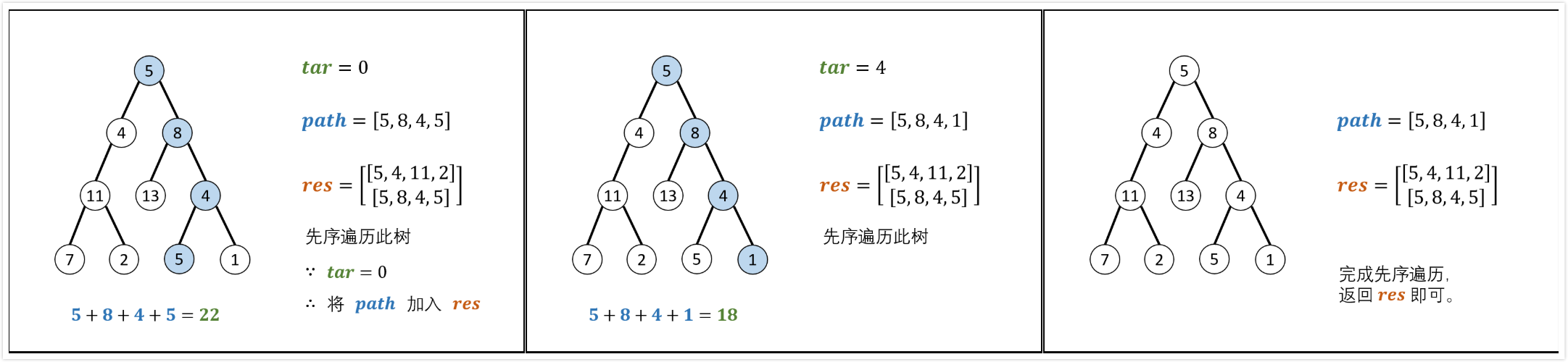
算法时间复杂度分析

时间复杂度$O(N)$：$N$为二叉树的节点数，先序遍历需要遍历所有节点。

C++代码

class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    vector<vector<int>> pathSum(TreeNode* root, int sum) {
		recur(root, sum);
        return res;
    }
    void recur(TreeNode* root, int tar){
        if(root == nullptr) return;
        path.push_back(root->val);
        tar -= root->val;
        if(tar == 0 && root->left == nullptr && root->right == nullptr) res.push_back(path);
        recur(root->left, tar);
        recur(root->right, tar);
        path.pop_back();
    }
};

复杂链表的复刻

请实现一个函数可以复制一个复杂链表。在复杂链表中，每个结点除了有一个指针指向下一个结点外，还有一个额外的指针指向链表中的任意结点或者null。

样例

1 2	输入：head = [[7,null],[13,0],[11,4],[10,2],[1,0]] 输出：[[7,null],[13,0],[11,4],[10,2],[1,0]]

思路

优化的迭代

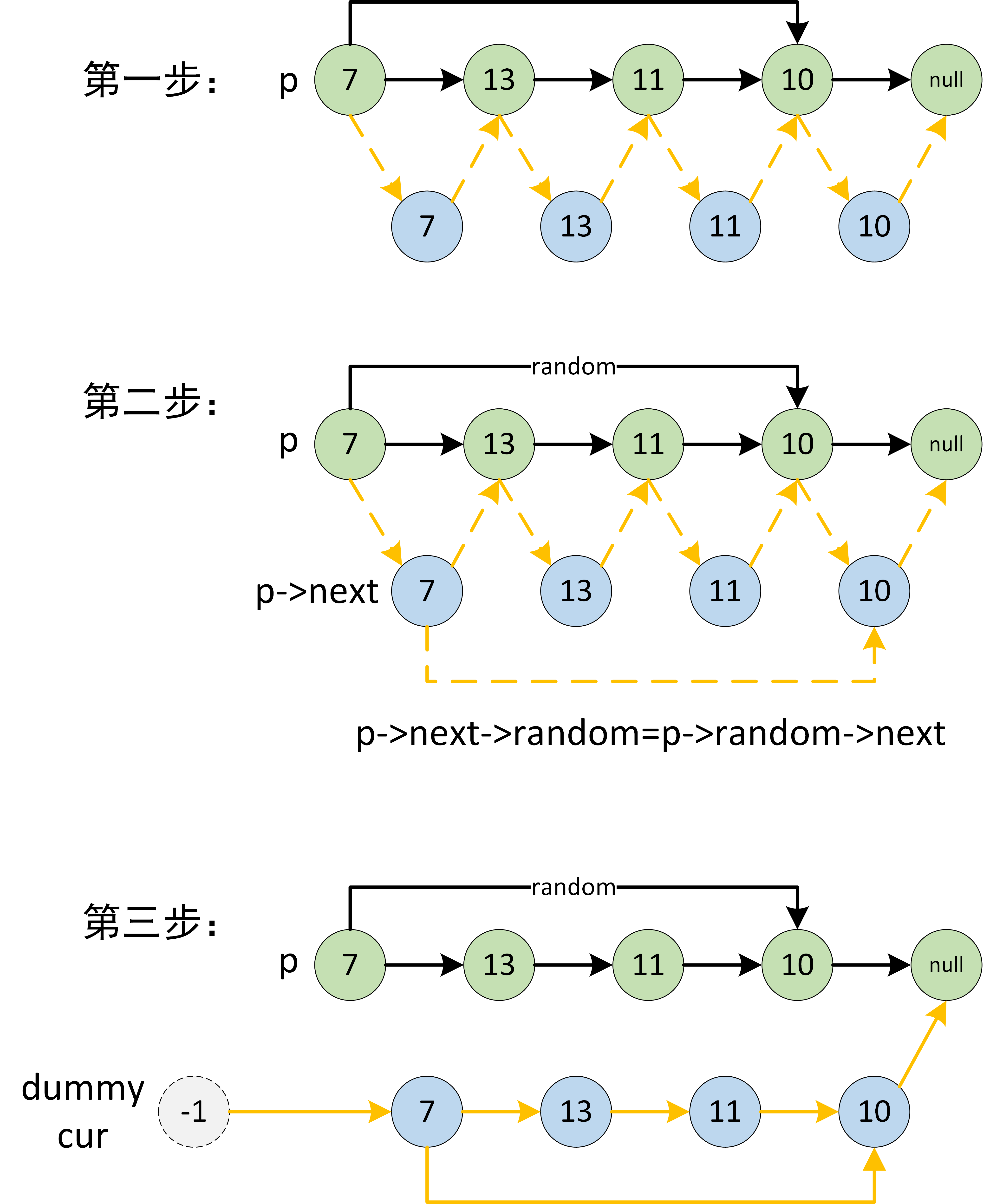
算法时间复杂度

时间复杂度：$O(N)$。

C++代码

class Solution {
public:
    Node* copyRandomList(Node* head) {
        if(head == nullptr) return nullptr;
        // 插入新复制的链表到每个原始链表节点的后边
        Node* p = head;
        while(p){
            Node* np = new Node(p->val);
            np->next = p->next;
            p->next = np;
            p = np->next;
        }
        // 根据原始链表的random，设置新链表的random
        p = head;
        while(p){
            if(p->random == nullptr) p->next->random = nullptr;
            else p->next->random = p->random->next;
            p = p->next->next;
        }
        // 分离新旧链表
        p = head;
        Node* dummy = head->next;
        Node* cp = dummy;
        while(p){
            p->next = p->next->next;
            p = p->next;
            if(p) cp->next = p->next;
            cp = cp->next;
        }

        return dummy;
    }
};

二叉搜索树与双向链表

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点，只能调整树中结点指针的指向。

注意：

需要返回双向链表最左侧的节点。

样例

输入下图中左边的二叉搜索树，则输出右边的排序双向链表。

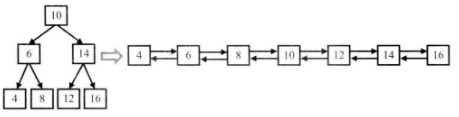
思路

中序遍历

二叉搜索树中序遍历序列为升序，将其转换为排序的循环双链表，包括：

排序链表：节点从小到大排序，应使用中序遍历访问数的节点；
双向链表：构建相邻节点（前驱节点$pre$，当前节点$cur$）关时，不仅应pre->right=cur，还需要cur->left=pre
循环链表：设置链表头节点$head$和尾节点$tail$，应建立head->left=tai，tail->right=head。

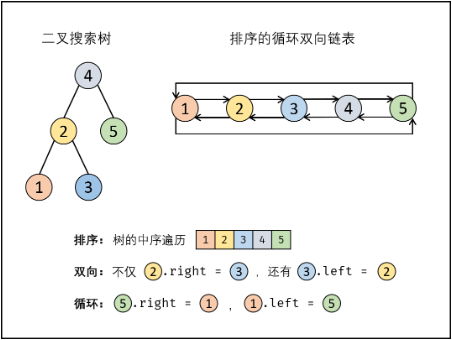
流程：

dfs(cur)中序遍历：

终止条件：当节点cur为空，代表节点越过叶节点，直接返回
递归左子树，即 dfs(cur.left) ；
构建链表：
1. 当$pre$为空时： 代表正在访问链表头节点，记为$head$。
2. 当$pre$不为空时：修改双向节点引用，即pre.right = cur，cur.left = pre；
3. 保存$cur$： 更新pre = cur，即节点cur是后继节点的pre；
递归右子树，即 dfs(cur.left) ；

treeToDoublyList(root)：
特例处理： 若节点root为空，则直接返回；
初始化： 空节点pre；
转化为双向链表： 调用dfs(root)；
构建循环链表： 中序遍历完成后，head指向头节点，pre指向尾节点，因此修改head和pre的双向节点引用即可。
返回值： 返回链表的头节点head即可。

算法时间发杂度

时间复杂度$O(N)$： $N$为二叉树的节点数，中序遍历需要访问所有节点。

C++代码

class Solution {
public:
    Node *pre, *head;
    Node* treeToDoublyList(Node* root) {
        if(root == nullptr) return null;
        dfs(root);
        head->left = pre;
        pre->right = head;
        return head;
    }
    void dfs(Node* cur){
        if(cur==nullptr) return;
        dfs(cur->left);
        if(pre!=nullptr) pre->right=cur;
        else head=cur;
        cur->left=pre;
        pre=cur;
        dfs(cur->right);
    }
};

序列化二叉树

请实现两个函数，分别用来序列化和反序列化二叉树。您需要确保二叉树可以序列化为字符串，并且可以将此字符串反序列化为原始树结构。

参考

样例

你可以序列化如下的二叉树
    8
   / \
  12  2
     / \
    6   4
为："[8, 12, 2, null, null, 6, 4, null, null, null, null]"

思路

二叉树的层次遍历

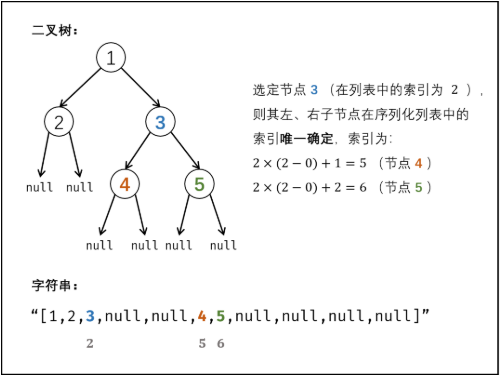
题目要求的 “序列化” 和 “反序列化” 是可逆操作。因此，序列化的字符串应携带 “完整的” 二叉树信息，即拥有单独表示二叉树的能力。

为使反序列化可行，考虑将越过叶节点后的$null$也看作是节点。在此基础上，对于列表中任意某节点$node$，其左子节点$node.left$和右子节点$node.right$在序列中的位置都是唯一确定的。

C++代码

/* 非层次遍历，用前序遍历序列，递归 */
class Codec {
public:
    string serialize(TreeNode* root) {
        string res;
        dfs_s(root,res);
        return res;
    }

    void dfs_s(TreeNode* root, string &res){
        if(root == nullptr){
            res+="null ";
            return; 
        }
        res += to_string(root->val) + ' ';
        dfs_s(root->left, res);
        dfs_s(root->right, res);
    }
    TreeNode* deserialize(string data) {
        int u = 0;
        return dfs_d(data,u);
    }
    
    TreeNode* dfs_d(string data, int &u){
        if(u == data.size()) return nullptr;
        int k = u;
        while(data[k]!=' ') k++;
        if(data[u]=='n'){
            u=k+1;
            return nullptr;
        }
        int val = 0;
        if(data[u] == '-'){
            for (int i = u+1; i < k; i++) val = val * 10 + data[i] - '0';
                val  = -val;
            }
            else{
            //如果是数字是正的
            for (int i = u; i < k; i++) val = val * 10 + data[i] - '0';
        }
        u = k+1;
        auto root = new TreeNode(val);
        root->left=dfs_d(data,u);
        root->right=dfs_d(data,u);
        return root;
    }
};

字符串排列

输入一个字符串，打印出该字符串中字符的所有排列。你可以以任意顺序返回这个字符串数组，但里面不能有重复元素。

1 2	输入：s = "abc" 输出：["abc","acb","bac","bca","cab","cba"]

思路

回溯法

排列方案的生成方法： 根据字符串排列的特点，考虑深度优先搜索所有排列方案。即通过字符交换，先固定第1位字符（n种情况）、再固定第2位字符（n−1种情况）、… 、最后固定第n位字符（1种情况）。

重复方案与剪枝：当字符串存在重复字符时，排列方案中也存在重复方案。为排除重复方案，需在固定某位字符时，保证 “每种字符只在此位固定一次” ，即遇到重复字符时不交换，直接跳过。从 DFS 角度看，此操作称为 “剪枝” 。

终止条件：当$x=len(c)-1$时，代表所有位已经固定（最后只有一种情况），则将当前组合c转化为字符串并加入res，返回。
递归参数：当前固定位x
递归工作：初始化一个set，用于排除重复的字符；将第x位字符与$i\in[x,len(c)]$字符分别交换，并进入下一层递归；
1. 剪枝：若$c[i]$在Set中，代表其是重复字符，因此需要剪枝；
2. 将$c[i]$加入Set，以便之后遇到重复字符时剪枝；
3. 固定字符：将字符$c[i]$和$c[x]$交换，即固定$c[i]$位当前字符；
4. 开启下层递归：调用$dfs(x+1)$，即开始固定$(x+1)$个字符；
5. 还原交换：将字符$c[i]$和$c[x]$交换（还原之前的交换）

算法时间复杂度

时间复杂度$O(N!)$： $N$为字符串$s$的长度；时间复杂度和字符串排列的方案数成线性关系，方案数为$N \times (N-1) \times (N-2) … \times 2 \times 1$，因此复杂度为$O(N!)$ 。

C++代码

class Solution {		// 只通过了50%
public:
    vector<string>res;
    vector<string> Permutation(string s) {
        int cursor=0;
        permutation(s,cursor);
        return res;
    }
    void permutation(string &s,int cursor){
        if(cursor==s.size()-1){				// 满足条件
            res.push_back(s);				// 添加路径
        }
        else{
            for(int i=cursor;i<s.size();i++){	// 选择列表 
                if(judge(s,cursor,i))continue;  // 从cursor开始，遍历不重复的字符
                swap(s[cursor],s[i]);			// 做选择
                permutation(s,cursor+1);	    // 下一层决策树
                swap(s[cursor],s[i]);			// 撤销选择
            }
        }
    }
    bool judge(string& s, int start, int end) {
        for (int i = start; i < end; ++i) {
            if (s[i] == s[end]) return true;
        }
        return false;
    }
};

数组中出现次数超过一半的数字

数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。假设数组非空，并且一定存在满足条件的数字。

思考题：

假设要求只能使用$O(n)$的时间和额外$O(1)$的空间，该怎么做呢？

样例

1 2	输入：[1,2,1,1,3] 输出：1

思路

哈希表统计
数组排序
摩尔投票：构建正负抵消
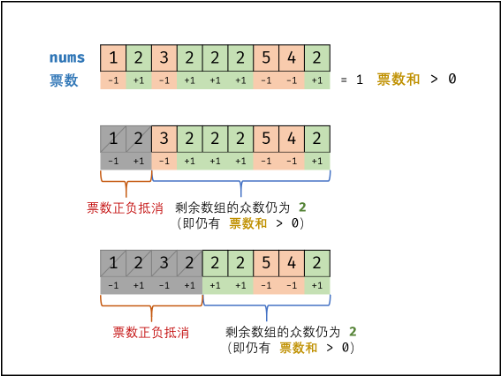
1. 票数和：由于众数出现的次数超过数组长度的一半；若记众数的票数为$+1$，非众数的票数为$−1$，则一定有所有数字的票数和$>0$。
2. 票数正负抵消：设数组nums中的众数为x，数组长度为n。若nums的前a个数字的票数和$=0$，则数组后(n−a)个数字的票数和一定仍$>0$（即后(n−a)个数字的众数仍为x）。

算法时间复杂度

时间复杂度$O(N)$ ：$N$为数组 nums 长度。

C++代码

class Solution {
public:
    int MoreThanHalfNum_Solution(vector<int> nums) {
        int x = 0, votes = 0, count = 0;       // x记录众数，votes记录票数
        for(int num : nums){
            if(votes == 0){
                x = num;
            }
            votes += num == x ? 1 : -1;
        }
        for(int num : nums)
            if(num == x) count++;
        return count > nums.size() / 2 ? x : 0; // 当无众数时返回 0
    }
};

最小的K个数

输入n个整数，找出其中最小的k个数。

注意：

数据保证k一定小于等于输入数组的长度;
输出数组内元素请按从小到大顺序排序;

样例

1 2	输入：[1,2,3,4,5,6,7,8] , k=4 输出：[1,2,3,4]

思路

优先队列，最小的K个数，大顶堆；最大的K个数，小顶堆

应该使用大顶堆来维护最小堆，而不能直接创建一个小顶堆并设置一个大小，企图让小顶堆中的元素都是最小元素。

维护一个大小为 K 的最小堆过程如下：在添加一个元素之后，如果大顶堆的大小大于 K，那么需要将大顶堆的堆顶元素去除。

算法时间复杂度

复杂度：$O(NlogK) + O(K)$

C++代码

class Solution {
public:
    vector<int> res;
    vector<int> getLeastNumbers(vector<int>& arr, int k) {
        if(k>arr.size())
            return res;
		priority_queue<int> heap;			// 申请一个堆
        for(auto x : arr){
            heap.push(x);					// 将元素放入堆
            if(heap.size()>k)				// 数组长度大于k，将对顶元素删除
                heap.pop();
        }
        while(heap.size()) res.push_back(heap.top()),heap.pop();
        return res;
    }
};

数据流的中位数

如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。

样例

1
2
3

输入：1, 2, 3, 4
输出：1,1.5,2,2.5
解释：每当数据流读入一个数据，就进行一次判断并输出当前的中位数。

思路

大小顶堆，

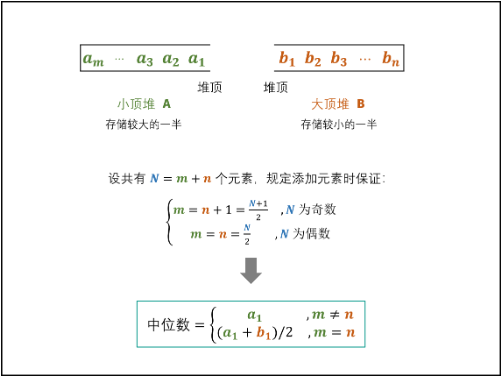
建立一个小顶堆$A$和一个大顶堆$B$，各保存列表的一般元素，且规定：

$A$保存较大的一半，长度位$\frac{N}{2}，(N为偶数)$或$\frac{N+1}{2}，(N为奇数)$；
$A$保存较小的一半，长度位$\frac{N}{2}，(N为偶数)$或$\frac{N-1}{2}，(N为奇数)$；

算法时间复杂度

时间复杂度：

查找中位数$O(1)$：获取堆顶元素使用$O(1)$时间；
添加数字$O(logN)$：堆的插入和弹出操作使用$O(logN)$时间。

C++代码

class Solution {
public:

    priority_queue<int> max_heap;
    priority_queue<int, vector<int>, greater<int> > min_heap;

    void Insert(int x){
        max_heap.push(x);
        if(min_heap.size() && max_heap.top() > min_heap.top())  // **1
        {
            auto maxv = max_heap.top(), minv = min_heap.top();
            max_heap.pop(), min_heap.pop();
            max_heap.push(minv), min_heap.push(maxv);
        }

        if(max_heap.size() > min_heap.size() + 1)
        {
            min_heap.push(max_heap.top());
            max_heap.pop();
        }
    }

    double GetMedian(){
        if((max_heap.size() + min_heap.size()) & 1) return max_heap.top();
        else return (max_heap.top() + min_heap.top()) / 2.0;
    }
};

连续子数组的最大和

输入一个非空整型数组，数组里的数可能为正，也可能为负。数组中一个或连续的多个整数组成一个子数组。求所有子数组的和的最大值。要求时间复杂度为O(n)。

样例

1 2	输入：[1, -2, 3, 10, -4, 7, 2, -5] 输出：18

思路

动态规划

状态定义：设动态规划列表$dp$ ，$dp[i]$代表以元素$nums[i]$为结尾的连续子数组最大和。
- 为何定义最大和$dp[i]$中必须包含元素$nums[i]$：保证$dp[i]$递推到$dp[i+1]$的正确性；如果不包含 $nums[i]$，递推时则不满足题目的连续子数组要求。
转移方程：若$dp[i-1] \leq 0$，说明$dp[i−1]$对$dp[i]$产生负贡献，即$dp[i−1]+nums[i]$还不如$nums[i]$本身大。
- $dp[i]=dp[i-1]+nums[i],dp[i-1]>0$
- $dp[i]=nums[i],dp[i-1]\leq0$
初始状态：$dp[0]=nums[0]$，即以$nums[0]$结尾的连续子数组最大和为$nums[0]$
返回值：返回$dp$列表中最大值

算法时间复杂度

时间复杂度$O(N)$： 线性遍历数组$nums$即可获得结果，使用$O(N)$时间。

C++代码

/*
s > 0: s + x;
s <=0: x;
*/
class Solution {
public:
    int FindGreatestSumOfSubArray(vector<int> nums) {
        int res = INT_MIN;
        int s = 0;
        for(auto x : nums){
            if(s < 0) s = 0;
            s += x;
            res = max(res, s);
        }
        return res;
    }
};

从1到n整数中1出现的次数

输入一个整数n，求从1到n这n个整数的十进制表示中1出现的次数。例如输入12，从1到12这些整数中包含“1”的数字有1，10，11和12，其中“1”一共出现了5次。

样例

1 2	输入： 12 输出： 5

思路

将$1 ~ n$的个位、十位、百位、…的1出现次数相加，即为1出现的总次数。

算法时间复杂度

C++代码

class Solution {
public:
    int NumberOf1Between1AndN_Solution(int n)
    {
        if(!n) return 0;
        vector<int> number;
        while(n) number.push_back(n % 10), n /= 10;
        int res = 0;
        for(int i = number.size() - 1; i >= 0; --i){
            auto left = 0, right = 0, t = 1;
            for(int j = number.size() - 1; j > i; --j) left = left * 10 + number[j];
            for(int j = i - 1; j >= 0; --j) right = right * 10 + number[j], t *= 10;
            res += left * t;
            if(number[i] == 1) res += right + 1;
            else if(number[i] >1) res += t;
        }
        return res;
    }
};