剑指Offer——Week5

发表于 | 分类于 |
字数统计: 3.7k | 阅读时长 ≈ 16

数字序列中某一位的数

数字以0123456789101112131415…的格式序列化到一个字符序列中。在这个序列中，第5位（从0开始计数）是5，第13位是1，第19位是4，等等。请写一个函数求任意位对应的数字。

样例

1
2
输入：13
输出：1

思路

递推

  1. 将$101112…$中的每一位称为数位，记为$n$；
  2. 将$10$、$11$、$12$、、、成为数字，记为$num$；
  3. 数字$10$是一个两位数，称此数的位数为$2$，记为$digit$；
  4. 每$digit$位数的起始数字（$10$、$11$、$12$、、、），记为$start$。

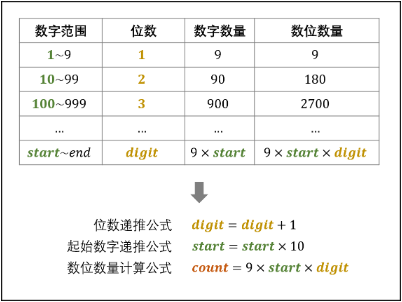
根据以上凡汐，可将其分解为三步：

  1. 确定$n$所在数字的位数，记为$digit$；

    • 循环执行$n$减去 一位数、两位数、… 的数位数量$count$，直至$n \leq count$时跳出。
    • 由于$n$已经减去了一位数、两位数、…、$(digit−1)$位数的数位数量$count$，因而此时的$n$是从起始数字$start$开始计数的。
    • 所求数位 ① 在某个$digit$位数中； ② 为从数字$start$开始的第$n$个数位。 
    1
    2
    3
    4
    5
    6
    digit = 1, start = 1, count = 9;
    while(n > count):
        n -= count
        start *= 10 # 1, 10, 100, ...
        digit += 1  # 1,  2,  3, ...
        count = 9 * start * digit # 9, 180, 2700, ...

  2. 确定$n$所在数字，记为$num$；

    • 所求数位的数字在从$start$开始的第$[(n - 1) / digit]$个数字中（$start$为第0个数字）
    • $num = start + (n - 1) // digit $

  3. 确定$n$是$num$中的哪一位，并返回。

    • 所求数位为数字$num$的第$(n - 1) \% digit$位（数字的首个数位为第0位）。 

      1
      2
      s = str(num) 						# 转化为 string
      res = int(s[(n - 1) % digit]) 		# 获得 num 的 第 (n - 1) % digit 个数位，并转化为 int

算法时间复杂度

时间复杂度$O(\log n)$： 所求数位$nn$对应数字$num$的位数$digit$最大为$O(\log n)$；第一步最多循环$O(logn)$次；第三步中将$num$转化为字符串使用$O(logn)$时间；因此总体为$O(logn)$。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int findNthDigit(int n) {
        int digit = 1;
        long start = 1;
        long count = 9;
        while (n > count) { // 1.
            n -= count;
            digit += 1;
            start *= 10;
            count = digit * start * 9;
        }
        long num = start + (n - 1) / digit; // 2.
        return to_string(num)[(n - 1) % digit] - '0'; // 3.
    }
};

把数组排成最小的数

输入一个正整数数组，把数组里所有数字拼接起来排成一个数，打印能拼接出的所有数字中最小的一个。例如输入数组[3, 32, 321]，则打印出这3个数字能排成的最小数字321323。

样例

1
2
输入：[3, 32, 321]
输出：321323

注意：输出数字的格式为字符串。

思路

定义新的排序规则

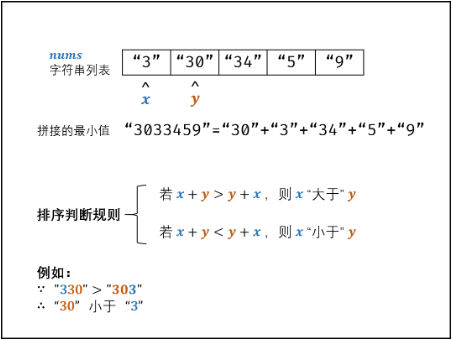
  1. 排序判断规则：设$nums$任意两数字的字符串格式为$x$和$y$，则：
    1. 若拼接字符串$x+y>y+x$，则$x>y$；
    2. 反之，若$x+y<y+x$，则$x<y$。
  2. 根据以上规则，套用任何排序方法对$nums$进行排序。

算法时间复杂度

时间复杂度$O(N \log N)$：$N$为最终返回值的字符数量（列表的长度$\leq N$）；使用快排或内置函数的平均时间复杂度为$O(NlogN)$，最差为$O(N^2)$。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    static bool cmp(int a, int b){
        string as = to_string(a), bs = to_string(b);
        return as + bs < bs + as;
    }
    string PrintMinNumber(vector<int> numbers) {
        sort(numbers.begin(), numbers.end(), cmp);
        string res;
        for(auto x : numbers)
            res += to_string(x);
        return res;
    }
};

把数字翻译成字符串

给定一个数字，我们按照如下规则把它翻译为字符串：0翻译成”a”，1翻译成”b”，……，11翻译成”l”，……，25翻译成”z”。一个数字可能有多个翻译。例如12258有5种不同的翻译，它们分别是”bccfi”、”bwfi”、”bczi”、”mcfi”和”mzi”。请编程实现一个函数用来计算一个数字有多少种不同的翻译方法。

样例

1
2
输入："12258"
输出：5

思路

动态规划

  1. 状态表示： 设动态规划列表$dp$，$dp[i]$代表以$x_i$为结尾的数字的翻译方案数量。

  2. 转移方程：若$x_i$和$x_{i-1}$组成的两位数字可以被翻译，则$dp[i] = dp[i - 1] + dp[i - 2]$；否则$dp[i] = dp[i - 1]$。

  1. 边界条件：初始状态： $dp[0]=dp[1]=1$，即 “无数字” 和 “第1位数字” 的翻译方法数量均为1；$dp[n]$ ，即此数字的翻译方案数量。

算法时间复杂度

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
/*
空间复杂度：O(1)
*/
class Solution {
public:
    int translateNum(int num) {
        string src = to_string(num);
        int p = 0, q = 0, r = 1;
        for (int i = 0; i < src.size(); ++i) {
            p = q; 
            q = r; 
            r = 0;
            r += q;
            if (i == 0) {
                continue;
            }
            auto pre = src.substr(i - 1, 2);
            if (pre <= "25" && pre >= "10") {
                r += p;
            }
        }
        return r;
    }
};

/*
空间复杂度：O(n)，遍历数组
*/
class Solution {
public:
    int translateNum(int num) {
        string s = to_string(num);
        int n = s.size();
        vector<int> arr(n + 1);
        arr[0] = 1;
        arr[1] = 1;
        for(int i = 2; i <= n; i++)
        {
            auto a = s.substr(i - 2, 2);
            if(a >= "10" && a <= "25")
                arr[i] = arr[i - 1] + arr[i - 2];
            else
                arr[i] = arr[i - 1];
        }
        return arr[n];
    }
};

礼物的最大价值

在一个m×n的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于0）。你可以从棋盘的左上角开始拿格子里的礼物，并每次向右或者向下移动一格直到到达棋盘的右下角。给定一个棋盘及其上面的礼物，请计算你最多能拿到多少价值的礼物？

注意：m,n>0m,n>0

样例

1
2
3
4
5
6
7
8
输入：
[
  [2,3,1],
  [1,7,1],
  [4,6,1]
]
输出：19
解释：沿着路径 2→3→7→6→1 可以得到拿到最大价值礼物。

思路

动态规划

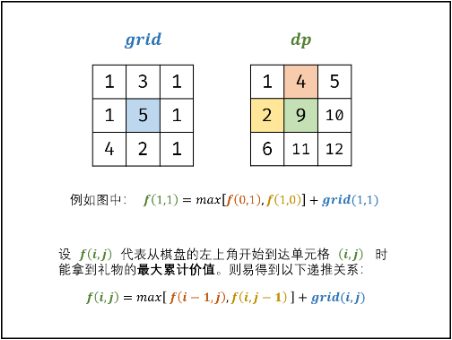
  1. 状态表示：$f[i,j]$——从左上角走到当前$[i,j]$处最大礼物累积

  2. 转移方程：$f[i,j]=max[f[i-1,j],f[i,j-1]]+grid[i,j]$

  3. 边界条件：

    • 初始状态：$f[0,0]=grid[0,0]$

    • 返回值：$f[m-1][n-1]$，$m,n$分别为矩阵的行高和列宽，即右下角。

算法时间复杂度

时间复杂度$O(MN)$： $M, N$分别为矩阵行高、列宽；动态规划需遍历整个$grid$矩阵，使用$O(MN)$时间。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int maxValue(vector<vector<int>>& grid) {
        int n = grid.size(), m = grid[0].size();
        vector<vector<int>> dp(n + 1, vector<int>(m + 1));
        for(int i = 1; i <= n; i++){
            for(int j = 1; j <= m; j++){
                dp[i][j] = max(dp[i][j - 1], dp[i - 1][j])+grid[i-1][j-1];
            }
        }
        return dp[n][m];
    }
};

最长不含重复字符的子字符串

请从字符串中找出一个最长的不包含重复字符的子字符串，计算该最长子字符串的长度。假设字符串中只包含从’a’到’z’的字符。

样例

1
2
输入："abcabc"
输出：3

思路

双指针

算法时间复杂度

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int lengthOfLongestSubstring(string s) {
		unordered_map<char,int> hash;
        int res = 0;
        for(int i = 0, j = 0; j < s.size(); j ++)
        {
            hash[s[j]] ++;
            while(hash[s[j]] > 1)
            {
                hash[s[i ++]] --;
            }
            res = max(res, j - i + 1);
        }
        return res;
    }
};

丑数

我们把只包含质因子2、3和5的数称作丑数（Ugly Number）。例如6、8都是丑数，但14不是，因为它包含质因子7。求第n个丑数的值。

样例

1
2
输入：5
输出：5

注意：习惯上我们把1当做第一个丑数。

思路

三路归并排序

1
2
3
nums2 = {1*2, 2*2, 3*2, 4*2, 5*2, 6*2, 8*2...}
nums3 = {1*3, 2*3, 3*3, 4*3, 5*3, 6*3, 8*3...}
nums5 = {1*5, 2*5, 3*5, 4*5, 5*5, 6*5, 8*5...}

包含2的除以2，包含3的除以3，包含5的除以5——判重合并（并集）之后可以得到丑数序列！！

判重：

算法时间复杂度

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int GetUglyNumber_Solution(int index) {
    	if (index < 7)return index;
        vector<int> res(index);
        res[0] = 1;
        int t2 = 0, t3 = 0, t5 = 0, i;
        for (i = 1; i < index; ++ i)
        {
            res[i] = min(res[t2] * 2, min(res[t3] * 3, res[t5] * 5));
            if (res[i] == res[t2] * 2) t2++;
            if (res[i] == res[t3] * 3) t3++;
            if (res[i] == res[t5] * 5) t5++;
        }
        return res[index - 1];
    }
};

字符串中第一个只出现一次的字符

在字符串中找出第一个只出现一次的字符。如输入"abaccdeff"，则输出b。如果字符串中不存在只出现一次的字符，返回#字符。

样例：

1
2
输入："abaccdeff"
输出：'b'

思路

模拟，哈希表

算法时间复杂度

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int FirstNotRepeatingChar(string str) {
        unordered_map<char, int> mp;
        for (const char ch : str) {
            ++ mp[ch];
        }     
        for (int i=0; i<str.length(); ++i) {
            if (mp[str[i]] == 1)
                return i;
        }
        return -1;
    }
};

字符流中第一个只出现一次的字符

请实现一个函数用来找出字符流中第一个只出现一次的字符。例如，当从字符流中只读出前两个字符”go”时，第一个只出现一次的字符是’g’。当从该字符流中读出前六个字符”google”时，第一个只出现一次的字符是’l’。如果当前字符流没有存在出现一次的字符，返回#字符。

样例

1
2
3
输入："google"
输出："ggg#ll"
解释：每当字符流读入一个字符，就进行一次判断并输出当前的第一个只出现一次的字符。

思路

双指针——队列，动态的过程

每次出现重复的字母，将其全部删掉

维护一个哈希表，记录从前往后字符出现的次数。

算法时间复杂度

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution
{
public:
    unordered_map<char, int> mp;
    queue<char> q;
    void Insert(char ch)
    {
         if (mp.find(ch) == mp.end()) {	
             q.push(ch);		// 如果是第一次出现， 则添加到队列中
         }
         ++mp[ch];				// 不管是不是第一次出现，都进行计数   
    }
  
    char FirstAppearingOnce()
    {
		while (!q.empty()) {
            char ch = q.front();// 拿出头部，如果是第一次出现，则返回
            if (mp[ch] == 1) {
                return ch;
            }
            else {
                q.pop();		// 不是第一次出现，则弹出，然后继续判断下一个头部
            }
        }
        return '#';
    }
};

数组的逆序对

在数组中的两个数字如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

样例

1
2
输入：[1,2,3,4,5,6,0]
输出：6

思路

归并排序

「归并排序」是分治思想的典型应用，它包含这样三个步骤：

算法时间复杂度

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
// 暴力—— 50%
class Solution {
public:
    int InversePairs(vector<int> data) {
        int res = 0;
        for(int i = 0; i < data.size(); i ++){
            for(int j = i + 1; j < data.size(); j ++){
                if(data[i] > data[j])
                    res ++;
            }
        }
        return res;
    }
};

// 归并排序
class Solution {
public:
    int getCount(vector<int>& nums, int begin, int end){
        if(begin == end) return 0;
        int mid = (begin + end) >> 1;        // 初始化中间位置
        vector<int> copy(nums);            // 辅助数组
        // 递归求解左右两边逆序对
        int leftCount = getCount(nums, begin, mid);
        int rightCount = getCount(nums, mid + 1, end);
        
        int crossCount = 0;                // 记录跨域两边的逆序对
        int i = mid, j = end, index = end;    // 前半部分、后半部分、辅助数组下标范围
        while(i >= begin && j > mid){
            if(nums[i] > nums[j]){            // 统计跨区逆序对
                copy[index --] = nums[i --];
                crossCount += j - begin - (mid - begin);    // 右边的减去左边的个数
            }
            else{
                copy[index --] = nums[j --];    // 不存在逆序对
            }
        }
        while(i >= begin)
            copy[index --] = nums[i --];
        while(j > mid)
            copy[index --] = nums[j --];
        for(int i = begin; i <= end; ++ i)
            nums[i] = copy[i];
        return (leftCount + rightCount + crossCount);
    }
    int InversePairs(vector<int> nums) {
        int n = nums.size();
        if(n < 2) return 0;
        else return getCount(nums, 0, n - 1);
    }
};

两个链表的第一个公共节点

输入两个链表，找出它们的第一个公共结点。当不存在公共节点时，返回空节点。

样例

1
2
3
4
5
6
7
给出两个链表如下所示：
A：        a1 → a2
                   ↘
                     c1 → c2 → c3
                   ↗            
B:     b1 → b2 → b3
输出第一个公共节点c1

思路

双指针

我们使用两个指针node1，node2分别指向两个链表headA，headB的头结点，然后同时分别逐结点遍历，当node1到达链表headA的末尾时，重新定位到链表headB的头结点；当node2到达链表headB的末尾时，重新定位到链表headA的头结点。这样，当它们相遇时，所指向的结点就是第一个公共结点。

算法时间复杂度

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    ListNode* FindFirstCommonNode( ListNode* pHead1, ListNode* pHead2) {
        ListNode *node1 = pHead1;
        ListNode *node2 = pHead2;
        
        while(node1 != node2){
            node1 = node1 != nullptr ? node1 -> next : pHead2;
            node2 = node2 != nullptr ? node2 -> next : pHead1;
        }
        return node1;
    }
};

数字在排序数组中出现的次数

统计一个数字在排序数组中出现的次数。例如输入排序数组[1, 2, 3, 3, 3, 3, 4, 5]和数字3，由于3在这个数组中出现了4次，因此输出4。

样例

1
2
输入：[1, 2, 3, 3, 3, 3, 4, 5] ,  3
输出：4

思路

二分法

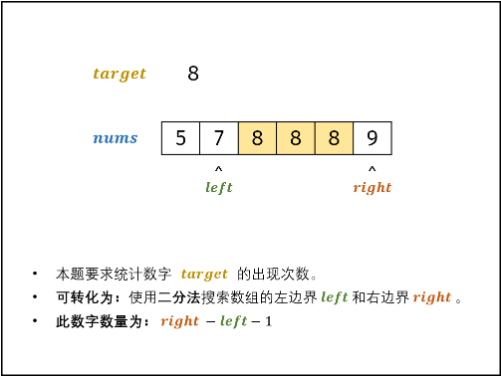
排序数组$nums$中的所有数字$target$形成一个窗口，记窗口的 左 / 右边界索引分别为$left$和$right$，分别对应窗口左边 / 右边的首个元素。

  1. 初始化：左边界$i=1$，右边界$r=nums.size() - 1$
  2. 循环二分：当闭区间$[i,j]$无元素就跳出来
    1. 计算中点$mid=(i+j)/2$
    2. 若$nums[mid]<target$，则$target$在闭区间$[mid+1,j]$中，执行$l=mid+1$;
    3. 若$nums[mid] > target$，则$target$在闭区间$[i,mid−1]$中，因此执行$j = mid - 1$；
    4. 若$nums[m] = target$，则右边界$right$在闭区间$[mid+1,j]$中；左边界$left$在闭区间$[i,mid-1]$中。因此分为以下两种情况：
      1. 若查找右边界$right$，则执行$i = mid + 1$；（跳出时$i$指向右边界）
      2. 若查找左边界$left$，则执行$j = mid - 1$；（跳出时$j$指向左边界）
  3. 返回值： 应用两次二分，分别查找$right$和$left$，最终返回$right - left - 1$即可。

算法时间复杂度

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int GetNumberOfK(vector<int> nums ,int k) {
        if(nums.empty()) return 0;
        int l = 0, r = nums.size() - 1;
        while(l < r){
            int mid = l + r >> 1;
            if(nums[mid] < k) l = mid + 1;
            else r = mid;
        }
        if(nums[l] != k) return 0;
        int left = l;
        
        l = 0, r = nums.size() - 1;
        while(l < r){
            int mid = l + r + 1 >> 1;
            if(nums[mid] <= k) l = mid;
            else r = mid - 1;
        }
        return r - left +1;
    }
};
-------------本文结束 感谢您的阅读-------------

本文标题:剑指Offer——Week5

文章作者:善雯

发布时间:2020年07月23日 - 10:07

最后更新:2020年07月23日 - 21:07

原始链接:http://shanwenyang.github.io/2020/07/23/Offer-Week5/

许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。

原创技术分享，您的支持将鼓励我继续创作
0%