Offer-Week6

发表于 | 分类于 |
字数统计: 2.9k | 阅读时长 ≈ 12

0到n-1中缺失的数字

一个长度为n-1的递增排序数组中的所有数字都是唯一的，并且每个数字都在范围0到n-1之内。在范围0到n-1的n个数字中有且只有一个数字不在该数组中，请找出这个数字。

样例

1
2
输入：[0,1,2,4]
输出：3

思路

优化时间复杂度，高斯公式——等差数列求和

二分查找

  1. 左子数组：$nums[i]=i$；
  2. 右子数组：$nums[i]\neq i$；

缺失数字等于右子数组的首元素对应的索引

  1. 初始化：左边界$i=0$，右边界$j=nums.size() - 1$；代表区间$[i,j]$
  2. 循环二分：当$i\leq j$时循环
    1. 计算中点$mid=(i+j)/2$
    2. 若$nums[mid]=mid$，则表示左子数组元素没有少，执行$i=mid+1$;
    3. 若$nums[mid]\neq mid$，则表示左子数组元素缺失，执行$j=mid-1$;
  3. 返回值：变量$i,j$分别指向右子数组首元素和左子数组末尾元素，返回$i$即可

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int missingNumber(vector<int>& nums) {
		int n = nums.size() + 1;
        int res = (n -1) * n / 2;
        for(auto x : nums) res -= x;
        return res;
    }
};

// 二分法
class Solution {
public:
    int missingNumber(vector<int>& nums) {
        int n = nums.size() - 1;
        int i = 0, j = n;
        while(i <= j){
            int mid = (i + j) >> 1;
            if(nums[mid] == mid) i = mid + 1;
            else j = mid - 1;
        }
        return i;
    }
};

数组中数值和下标相等的元素

假设一个单调递增的数组里的每个元素都是整数并且是唯一的。请编程实现一个函数找出数组中任意一个数值等于其下标的元素。例如，在数组[-3, -1, 1, 3, 5]中，数字3和它的下标相等。

样例

1
2
输入：[-3, -1, 1, 3, 5]
输出：3

注意:如果不存在，则返回-1。

思路

二分查找

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int getNumberSameAsIndex(vector<int>& nums) {
        int l = 0, r = nums.size() - 1;
        while(l < r){
            int mid = l + r >> 1;
            if(nums[mid] - mid >= 0) r = mid;
            else l = mid + 1;
        }
        if(nums[r] - r ==0) return r;
        else return -1;
    }
};

二叉搜索树的第k个结点

给定一棵二叉搜索树，请找出其中的第k小的结点。你可以假设树和k都存在，并且1≤k≤树的总结点数。

样例

1
2
3
4
5
输入：root = [2, 1, 3, null, null, null, null] ，k = 3
    2
   / \
  1   3
输出：1

思路

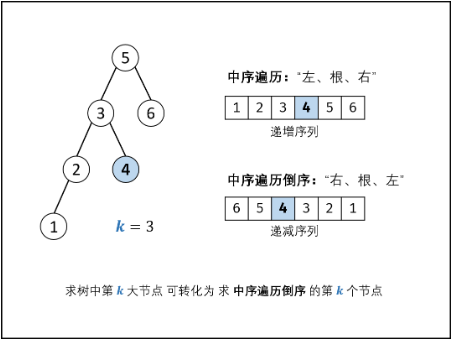
二叉搜索树的中序遍历为 递增序列 。

二叉搜索树的中序遍历的倒序（右、根、左）为 递减序列 。

求“二叉搜索树第$k$大的节点”可转化为求“此树的中序遍历倒序的第$k$个节点”。

  1. 终止条件：当结点为空时，返回
  2. 递归右子树：$dfs(root->right)$
  3. 三项工作：
    1. 提前返回：若$k=0$，代表已经找到目标结点，无需继续遍历，返回
    2. 统计序号：执行$k—$
    3. 记录结果：若$k=0$，代表当前节点为第$k$大的结点，记录$res=root->val$
  4. 递归左子树：$dfs(root->left)$

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
public:
    int res;
    int kthLargest(TreeNode* root, int k) {
		dfs(root, k);
        return res;
    }
    void dfs(TreeNode* root, int &k){
        if(root == nullptr) return;
        dfs(root->right, k);
        -- k;
        if(!k) res = root -> val;
        dfs(root -> left, k);
    }
};

// 非递归方式
class Solution {
public:
    TreeNode* KthNode(TreeNode* pRoot, int k) {
        stack<TreeNode*> stk;
        TreeNode* cur = pRoot;
        while(cur || stk.size()) {
            while(cur) {
                stk.push(cur);
                cur = cur->left;
            }
            cur = stk.top();
            stk.pop();
            if(-- k == 0) return cur;
            cur = cur->right;
        }
        return nullptr;
    }
};

二叉树的深度

输入一棵二叉树的根结点，求该树的深度。从根结点到叶结点依次经过的结点（含根、叶结点）形成树的一条路径，最长路径的长度为树的深度。

样例

1
2
3
4
5
6
7
输入：二叉树[8, 12, 2, null, null, 6, 4, null, null, null, null]如下图所示：
    8
   / \
  12  2
     / \
    6   4
输出：3

思路

递归

后序遍历：

  • 树的后序遍历 / 深度优先搜索往往利用 递归 或 栈 实现，本文使用递归实现。

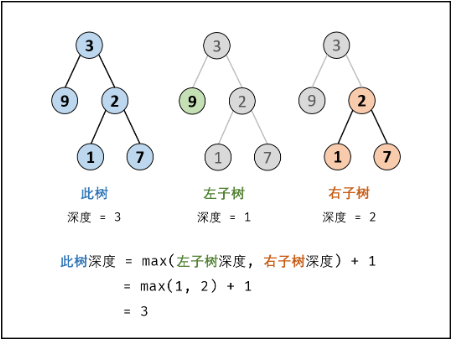
  • 关键点： 此树的深度和其左（右）子树的深度之间的关系。显然，此树的深度 等于 左子树的深度 与 右子树的深度 中的 最大值 +1 。

算法解析：

  1. 终止条件： 当root为空，说明已越过叶节点，因此返回深度0。
  2. 递推工作： 本质上是对树做后序遍历。
    1. 计算节点root的左子树的深度 ，即调用maxDepth(root.left)
    2. 计算节点root的右子树的深度 ，即调用maxDepth(root.right)
  3. 返回值： 返回 此树的深度 ，即max(maxDepth(root.left), maxDepth(root.right)) + 1。

层次遍历：

  • 树的层序遍历 / 广度优先搜索往往利用 队列 实现。
  • 关键点： 每遍历一层，则计数器+1，直到遍历完成，则可得到树的深度。

算法解析：

  1. 特例处理： 当root为空，直接返回深度0。
  2. 初始化： 队列queue（加入根节点root），计数器res = 0。
  3. 循环遍历： 当queue为空时跳出。
    1. 初始化一个空列表tmp，用于临时存储下一层节点；
    2. 遍历队列： 遍历queue中的各节点node，并将其左子节点和右子节点加入tmp；
    3. 更新队列： 执行queue = tmp，将下一层节点赋值给queue；
    4. 统计层数： 执行res += 1，代表层数加1
  4. 返回值： 返回res 即可。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// 后序遍历
class Solution {
public:
    int TreeDepth(TreeNode* pRoot)
    {
        if(!root) return 0;
        return max(TreeDepth(root -> left),TreeDepth(root -> right)) + 1;
    }
};

// 层次遍历
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == nullptr) return 0;
        queue<TreeNode*> q;
        q.push(root);
        int res = 0;
        while (!q.empty()) {
            res++;
            int n = q.size();
            for (int i = 0; i < n; i++) {
                TreeNode* node = q.front();
                q.pop();
                if (node->left != nullptr) q.push(node->left);
                if (node->right != nullptr) q.push(node->right);
            }
        }
        return res;
    }
};

平衡二叉树

输入一棵二叉树的根结点，判断该树是不是平衡二叉树。如果某二叉树中任意结点的左右子树的深度相差不超过1，那么它就是一棵平衡二叉树。

注意：

  • 规定空树也是一棵平衡二叉树。

样例

1
2
3
4
5
6
7
输入：二叉树[5,7,11,null,null,12,9,null,null,null,null]如下所示，
    5
   / \
  7  11
    /  \
   12   9
输出：true

思路

遇上一题类似

以下两种方法均基于以下性质推出：此树的深度 等于左子树的深度与右子树的深度中的最大值+1。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 后序遍历
class Solution {
public:
    bool ans = true;
    bool IsBalanced_Solution(TreeNode* root) {
		dfs(root);
        return ans;
    }
    int dfs(TreeNode* root){
        if(!root) return 0;
        int left = dfs(root -> left), right = dfs(root -> right);
        if(abs(left - right) > 1) ans = false;
        return max(left, right) + 1;
    }
};

数组中只出现过一次的两个数字

一个整型数组里除了两个数字之外，其他的数字都出现了两次。请写程序找出这两个只出现一次的数字。你可以假设这两个数字一定存在。

样例

1
2
输入：[1,2,3,3,4,4]
输出：[1,2]

思路

位运算，分组异或操作

  1. 将所有数进行异或操作，得到x^y的结果
  2. 找到x^y的第k位为1
  3. 根据第k位为0或1的情况，将数组分成两个集合（x和y分别位于两个集合）
  4. 对两个集合再次进行异或操作，得到x和y

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    void FindNumsAppearOnce(vector<int> data,int* num1,int *num2) {
        int sum = 0;
        for(auto x : data) sum ^= x;
        int k = 0;
        while(!(sum >> k & 1)) k ++;
        *num1 = 0, *num2 = 0;
        for(auto x : data)
            if(x >> k & 1)
                *num1 ^= x;
        *num2 = *num1 ^ sum;
    }
};

数组中唯一只出现一次的数字

在一个数组中除了一个数字只出现一次之外，其他数字都出现了三次。请找出那个只出现一次的数字。你可以假设满足条件的数字一定存在。

思考题：

  • 如果要求只使用O(n)的时间和额外O(1)的空间，该怎么做呢？

样例

1
2
输入：[1,1,1,2,2,2,3,4,4,4]
输出：3

思路

二进制，有限状态机

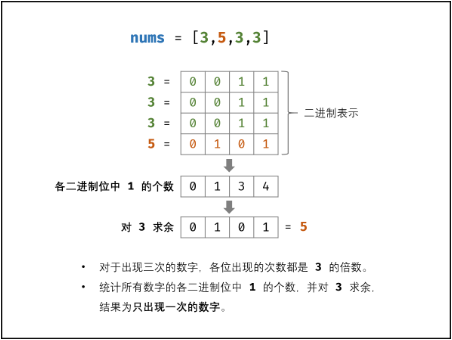
  1. 对于出现三次的数字，各二进制位出现的次数都是3的倍数。
  2. 统计所有数字的各二进制位中1的出现次数，并对3求余，结果则为只出现一次的数字。

C++代码

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int ones = 0, twos = 0;
        for(auto x : nums){
            ones = (ones ^ x) & ~twos;
            twos = (twos ^ x) & ~ones;
        }
        return ones;
    }
};

和为S的两个数字

输入一个数组和一个数字s，在数组中查找两个数，使得它们的和正好是s。如果有多对数字的和等于s，输出任意一对即可。你可以认为每组输入中都至少含有一组满足条件的输出。

样例

1
2
输入：[1,2,3,4] , sum=7
输出：[3,4]

思路

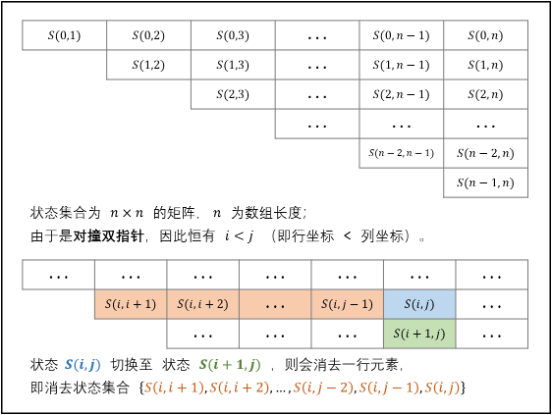
双指针

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
// 哈希
class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_set<int> hash;
        for(int i = 0; i < nums.size(); i ++){
            if(hash.count(target - nums[i]))
                return vector<int> {target - nums[i], nums[i]};
            hash.insert(nums[i]);
        }
        return vector<int>();
    }
};
// 双指针
class Solution {
public:
    vector<int> FindNumbersWithSum(vector<int> nums,int target) {
        if(nums.size() < 1) return {};
        int i = 0, j = nums.size() - 1;
        while(i < j){
            int sum = nums[i] + nums[j];
            if(sum > target)
                j --;
            else if(sum < target)
                i ++;
            else return vector<int>{nums[i],nums[j]};
        }
        return{};
    }
};

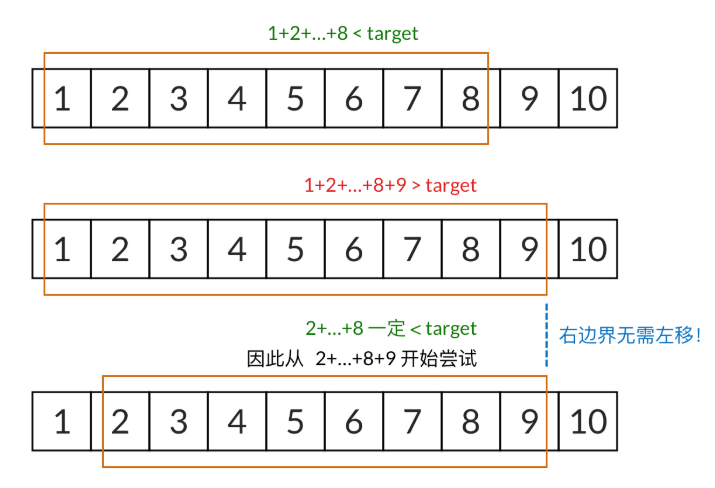
和为S的连续正整数序列

输入一个正数s，打印出所有和为s的连续正数序列（至少含有两个数）。例如输入15，由于1+2+3+4+5=4+5+6=7+8=15，所以结果打印出3个连续序列1～5、4～6和7～8。

样例

1
2
输入：15
输出：[[1,2,3,4,5],[4,5,6],[7,8]]

思路

双指针，滑动窗口

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    vector<vector<int> > FindContinuousSequence(int sum) {
        vector<vector<int>> res;
        for(int i = 1, j = 1, s = 1; i <= sum; i ++){
            while(s < sum) s += ++ j;
            if(s == sum && j - i + 1 > 1){
                vector<int> line;
                for(int k = i; k <= j; k ++) line.push_back(k);
                res.push_back(line);
            }
            
            s -= i;
        }
        return res;
    }
};

翻转单词顺序

输入一个英文句子，翻转句子中单词的顺序，但单词内字符的顺序不变。为简单起见，标点符号和普通字母一样处理。例如输入字符串"I am a student."，则输出"student. a am I"。

样例

1
2
输入："I am a student."
输出："student. a am I"

思路

双指针

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 双指针
class Solution {
public:
    string ReverseSentence(string str) {
        reverse(str.begin(), str.end());
        for(int i = 0; i < str.size(); i ++){
            int j = i;
            while(j < str.size() && str[j] != ' ') j ++;
            reverse(str.begin() + i, str.begin() + j);
            i = j;
        }
        return str;
    }
};

左旋转字符串

字符串的左旋转操作是把字符串前面的若干个字符转移到字符串的尾部。请定义一个函数实现字符串左旋转操作的功能。比如输入字符串"abcdefg"和数字2，该函数将返回左旋转2位得到的结果"cdefgab"。

注意：

  • 数据保证n小于等于输入字符串的长度。

样例

1
2
输入："abcdefg" , n=2
输出："cdefgab"

思路

操作分解

  1. 反转整个字符串序列
  2. 反转两个字符串子序列

C++代码

1
2
3
4
5
6
7
8
9
class Solution {
public:
    string LeftRotateString(string str, int n) {
        reverse(str.begin(),str.end());
        reverse(str.begin(), str.begin() + str.size() - n);
        reverse(str.begin() + str.size() - n, str.end());
        return str;
    }
};
-------------本文结束 感谢您的阅读-------------

本文标题:Offer-Week6

文章作者:善雯

发布时间:2020年07月27日 - 10:07

最后更新:2020年07月28日 - 12:07

原始链接:http://shanwenyang.github.io/2020/07/27/Offer-Week6/

许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。

原创技术分享，您的支持将鼓励我继续创作
0%