剑指Offer——Week7

发表于 | 分类于 |
字数统计: 2.3k | 阅读时长 ≈ 10

滑动窗口的最大值

给定一个数组 nums 和滑动窗口的大小 k，请找出所有滑动窗口里的最大值。

样例

1
2
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]

思路

单调队列

存储下标

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        if(!nums.size()) return {};
        vector<int> res;
        deque<int> que;
        for(int i = 0; i < nums.size(); ++ i){
            // 把队列里面滑出过时的数剔除
            while(!que.empty() && i - que.front() >= k) que.pop_front();
            // 判断队列的单调性 小于当前值的全部pop
            while(!que.empty() && nums[i] >= nums[que.back()]) que.pop_back();
            // 更新队列
            que.push_back(i);
            // 记录答案
            if(i >= k) res.push_back(nums[que.front()]);
        }
        return res;
    }
};

骰子的点数

把n个骰子扔在地上，所有骰子朝上一面的点数之和为s。输入n，打印出s的所有可能的值出现的概率。你需要用一个浮点数数组返回答案，其中第 i 个元素代表这 n 个骰子所能掷出的点数集合中第 i 小的那个的概率。

样例

1
2
输入: 2
输出: [0.02778,0.05556,0.08333,0.11111,0.13889,0.16667,0.13889,0.11111,0.08333,0.05556,0.02778]

思路

动态规划

使得$n-1$点数概率数组和$1$点数概率数组元素两两相乘，并将乘积结果加到$n$点数概率数组上。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    vector<double> twoSum(int n) {
        int dp[15][70];
        memset(dp, 0, sizeof(dp));
        for (int i = 1; i <= 6; i ++) {
            dp[1][i] = 1;
        }
        for (int i = 2; i <= n; i ++) {
            for (int j = i; j <= 6*i; j ++) {
                for (int cur = 1; cur <= 6; cur ++) {
                    if (j - cur <= 0) {
                        break;
                    }
                    dp[i][j] += dp[i-1][j-cur];
                }
            }
        }
        int all = pow(6, n);
        vector<double> ret;
        for (int i = n; i <= 6 * n; i ++) {
            ret.push_back(dp[n][i] * 1.0 / all);
        }
        return ret;
    }
};

扑克牌的顺子

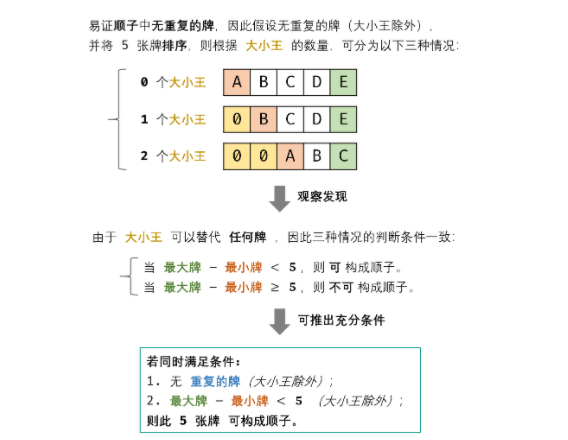
从扑克牌中随机抽5张牌，判断是不是一个顺子，即这5张牌是不是连续的。2～10为数字本身，A为1，J为11，Q为12，K为13，而大、小王为 0 ，可以看成任意数字。A 不能视为 14。

样例

1
2
输入: [1,2,3,4,5]
输出: True

思路

模拟

  1. 删除0
  2. 是否有重复
  3. 都不相同看最大和最小的差值是否在<=4

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
// 排序
class Solution {
public:
    bool isStraight(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        int k = 0;
        while(!nums[k]) k ++;							// 删除行首的 0
        for(int i = k + 1; i < nums.size(); i ++)		// k + 1 就是第一个非 0 的数
            if(nums[i] == nums[i - 1]) return false;
        return nums.back() - nums[k] <= 4;
    }
};

// set
class Solution {
public:
    bool isStraight(vector<int>& nums) {
        set<int> repeat;
        int ma = 0, mi = 14;
        for(int n : nums){
            if(n == 0) continue;
            ma = max(ma, n);
            mi = min(mi, n);
            if (repeat.find(n) != repeat.end()) return false;
            repeat.insert(n);
        }
        return ma - mi < 5;
    }
};

圆圈中最后剩下的数字

0,1,,,n-1这n个数字排成一个圆圈，从数字0开始，每次从这个圆圈里删除第m个数字。求出这个圆圈里剩下的最后一个数字。

样例

1
2
输入: n = 5, m = 3
输出: 3

思路

约瑟夫环

暴力，略

递推：寻找相邻两个数的关系——$f(n,m) = (f(n-1,m)+m)\%n$，$f(1,m)=0$

删除第m个数的下标是m-1；对剩下的数重新编号；旧编号：m，m+1，m+2…；新编号：0，1，2…；有编号规则：（新 + m）% n

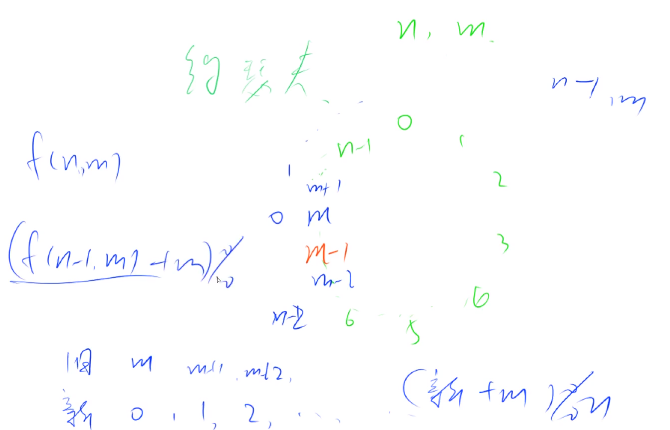
代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 递归
class Solution {
public:
    int lastRemaining(int n, int m) {
        if(n == 1) return 0;
        return (lastRemaining(n - 1, m) + m) % n;
    }
};
// 暴力
class Solution {
public:
    int lastRemaining(int n, int m) {
        if(m == 0 || n == 0) return -1;
        int ans = 0;
        // 最后一轮剩下2个人，所以从2开始反推
        for (int i = 2; i <= n; i++) {
            ans = (ans + m) % i;
        }
        return ans;
    }
};

股票的最大利润

假设把某股票的价格按照时间先后顺序存储在数组中，请问买卖该股票一次可能获得的最大利润是多少？

样例

1
2
3
4
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。

思路

枚举：枚举在哪一天卖，用minv记录前 i 天的股票价格最小值（可降低时间复杂度）。

代码

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int maxProfit(vector<int>& nums) {
        int res = 0;
        for (int i = 0, minv = INT_MAX; i < nums.size(); i ++ ) {
            if (minv < nums[i])
                res = max(res, nums[i] - minv);
            minv = min(minv, nums[i]);
        }
        return res;
    }
};

求1+2+…+n

求 1+2+...+n ，要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句（A?B:C）。

思路

语法题

  1. 通向公式——不可以
  2. for(1~n)——不可以
  3. dfs(){if…}——不可以
  4. if(A && B)：只要A为false就不会再执行；if(A||B)如果A为true，不管B直接执行；利用这个性质：

代码

1
2
3
4
5
6
7
8
9
class Solution {
public:
    int sumNums(int n) {
        int res = n;
        // if(n > 0) res += sumNums(n - 1); 利用性质将if判断去掉
        n > 0 && (res += sumNums(n - 1));
        return res;
    }
};

不用加减乘除做加法

写一个函数，求两个整数之和，要求在函数体内不得使用 “+”、“-”、“*”、“/” 四则运算符号。

思路

位运算

计算机只有&、|、~、^（由前三种组合运算）。

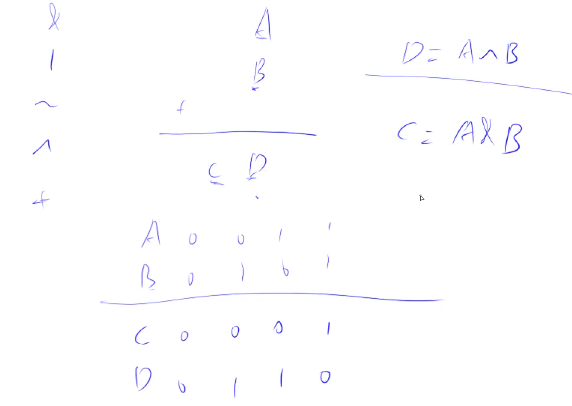
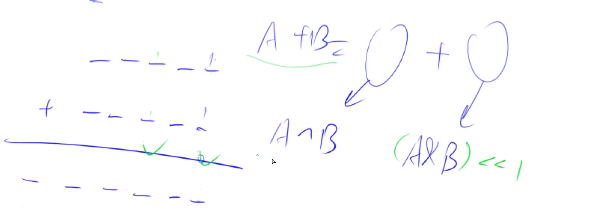
多位数相加，一般串行，但是亦可以并行计算。A+B可拆分为进位和+非进位和两部分

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int add(int a, int b) {
        int sum, carry;
        while (b != 0) {
            // 异或操作得无进位和
            sum = a ^ b;
            // 与操作后移位得进位值
            carry = ((unsigned int) (a & b) << 1);
            // 循环，直到进位为0
            a = sum;
            b = carry;
        }
    return a;
    }
};

构建乘积矩阵

给定一个数组 A[0,1,…,n-1]，请构建一个数组 B[0,1,…,n-1]，其中 B 中的元素 B[i]=A[0]×A[1]×…×A[i-1]×A[i+1]×…×A[n-1]。不能使用除法。

样例

1
2
输入: [1,2,3,4,5]
输出: [120,60,40,30,24]

思路

image-20200903172808303

$B_i=\frac{\sum^{n-1}_{i=0}A_i}{A_i}$，想一个循环顺序：先让$B_i$等于左边乘积，再让$B_i$等于右边乘积（倒着），再相乘。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    vector<int> constructArr(vector<int>& A) {
        if (A.empty()) return vector<int>();
        int n = A.size();
        vector<int> res(n);
        res[0] = 1;
        for (int i = 1, p = A[0]; i < n; i ++ ) {
            res[i] = p;
            p *= A[i];
        }
        for (int i = n - 2, p = A[n - 1]; i >= 0; i -- ) {
            res[i] *= p;
            p *= A[i];
        }
        return res;
    }
};

把字符串转换成整数

写一个函数StrToInt，实现把字符串转换成整数这个功能。不能使用atoi或者其他类似的库函数。

样例

1
2
输入: "42"
输出: 42

思路

模拟

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int strToInt(string str) {
        int i = 0, flag = 1;
        long res = 0; 			//默认flag = 1，正数
        while (str[i] == ' ') i ++;
        if (str[i] == '-') flag = -1;
        if (str[i] == '-' || str[i] == '+') i ++;
        for (; i < str.size() && isdigit(str[i]); i ++)  {
            res = res * 10 + (str[i] - '0');
            if (res >= INT_MAX && flag == 1) return  INT_MAX;
            if (res > INT_MAX && flag == -1) return  INT_MIN;
        } 
        return flag * res;
    }
};

二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

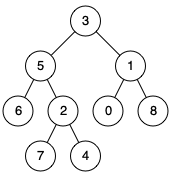
样例

1
2
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3

思路

根据以上定义，若 rootroo**t 是 p, qp,q 的 最近公共祖先 ，则只可能为以下情况之一：

  1. $p$和$q$在$root$的子树中，且分列$root$的异侧（即分别在左、右子树中）；
  2. $p = root$，且 $q$在$root$的左或右子树中；
  3. $q = root$，且 $p$在$root$的左或右子树中；

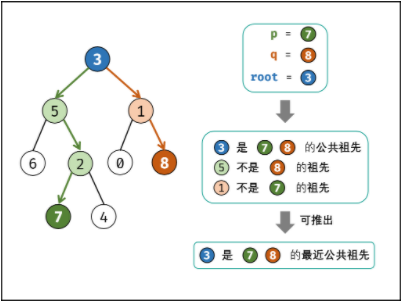
考虑通过递归对二叉树进行后序遍历，当遇到节点$p$或$q$时返回。从底至顶回溯，当节点$p$, $q$在节点$rootR$的异侧时，节点$root$即为最近公共祖先，则向上返回$root$。

递归解析：

  1. 终止条件：

    1. 当越过叶节点，则直接返回null；
    2. 当root等于p, q，则直接返回root；

  2. 递推工作：

    1. 开启递归左子节点，返回值记为left；
    2. 开启递归右子节点，返回值记为right；

  3. 返回值： 根据left和right，可展开为四种情况；

    1. 当left和right同时为空 ：说明root的左 / 右子树中都不包含p，q,返回 null；
    2. 当left和right同时不为空 ：说明p，q分列在root的异侧（分别在 左 / 右子树），因此root为最近公共祖先，返回root；

    3. 当left为空 ，right不为空 ：p，q都不在root的左子树中，直接返回right。具体可分为两种情况：

      1. p，q其中一个在root的右子树中，此时right指向p（假设为p）；
      2. p，q两节点都在root的右子树中，此时的right指向最近公共祖先节点 ；

    4. 当left不为空， right：与情况 3. 同理；

代码

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root == nullptr || p == root || q == root) return root;
        auto left = lowestCommonAncestor(root -> left, p, q);
        auto right = lowestCommonAncestor(root -> right, p, q);
        if(left && right) return root;
        else return left ? left : right;
    }
};
-------------本文结束 感谢您的阅读-------------

本文标题:剑指Offer——Week7

文章作者:善雯

发布时间:2020年09月02日 - 20:09

最后更新:2020年09月04日 - 14:09

原始链接:http://shanwenyang.github.io/2020/09/02/Offer-Week7/

许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。

原创技术分享，您的支持将鼓励我继续创作
0%